5.10.23
Zwei unabhängige DDS-Generatoren erzeugen zwei fast identische Sinusschwingen, die sich kaum durch ihre Frequenz unterscheiden. Stellt man das eine Signal auf der x-Achse des Oszilloskops dar und das andere Signal auf der y-Achse dar, erhält man Lissajous-Figuren, die sich langsam drehend eine anmutige Erscheinung darstellen. Dazu enthält dieser Artikel viele Videos als Anschauungsmaterial.

Lissajous-Figuren sind komplexe, sich wiederholende Muster, die durch die Überlagerung von harmonischen Schwingungen entstehen. Diese Figuren wurden nach dem französischen Mathematiker Jules Antoine Lissajous benannt, der im 19. Jahrhundert lebte. Lissajous studierte die Bewegungen von mechanischen Systemen und untersuchte die Beziehungen zwischen verschiedenen Schwingungen. Die Muster, die heute als Lissajous-Figuren bekannt sind, wurden erstmals von ihm beschrieben und sind das Ergebnis der Überlagerung von zwei oder mehr sinusförmigen Wellen mit verschiedenen Frequenzen.
Lissajous-Figuren sind nicht nur mathematisch interessant, sondern haben auch Anwendungen in verschiedenen Bereichen wie Physik, Ingenieurwissenschaften, Musik und Kunst. Sie werden oft verwendet, um die Beziehungen zwischen verschiedenen Schwingungen zu visualisieren und zu verstehen.
Werden Vielfache einer Frequenz dargestellt, entstehen wunderschöne Gebilde, die sich langsam drehen, wenn die Frequenzen etwas von dem Vielfachen abweichen. Die kurzen Videos weiter unten im Artikel sollen dies darstellen.
Die Theorie dazu ist auf https://de.wikipedia.org/wiki/Lissajous-Figur erschöpfend erklärt.
Nachfolgend möchte ich meinen Versuchsaufbau aus der rauen Bastelpraxis und die Ergebnisse vorstellen.

Auf dem obigen Bild kommen zwei DDS-Generatoren zum Einsatz. Der oben im weißen Gehäuse untergebrachte basiert auf einem AD9850 und er Versuchsaufbau auf dem Tisch mit basiert auf einem AD9851. Beide sind anfangs auf 1 kHz eingestellt.
Bauanleitung DDS-Generator mit AD9850, 1 Hz – 40 MHz
Bauanleitung DDS-Generator mit AD9851, 1 Hz – 70 MHz



Da die beiden Generatoren nicht synchronisiert sind, liefern sie etwas abweichende Frequenzen. Dadurch drehen sich die Gebilde, was auf Video festgehalten wurde:
Obiges Video: Darstellung der zwei 1 kHz-Sinuskurven auf einem Zweikanal-Oszilloskop. Da die Frequenzen minimal abweichen, wandert die Sinuskurve des einen Kanals langsam weg.
Obiges Video: Beide Signale mit 1 Hz Abweichung werden addiert. Es entsteht eine Schwebung. Je nach Phasenlage heben sich die Schwingungen auf oder verstärken sich.
Obiges Video: Lissajous-Figur eines Kreises. Die Drehbewegung erscheint, weil die Frequenzabweichung minimal ist.
Obiges Video: Jetzt dreht sich der Kreis schneller, weil die Abweichung 1 Hz beträgt.
Obiges Video: Frequenzverhältnis nahezu 1:2
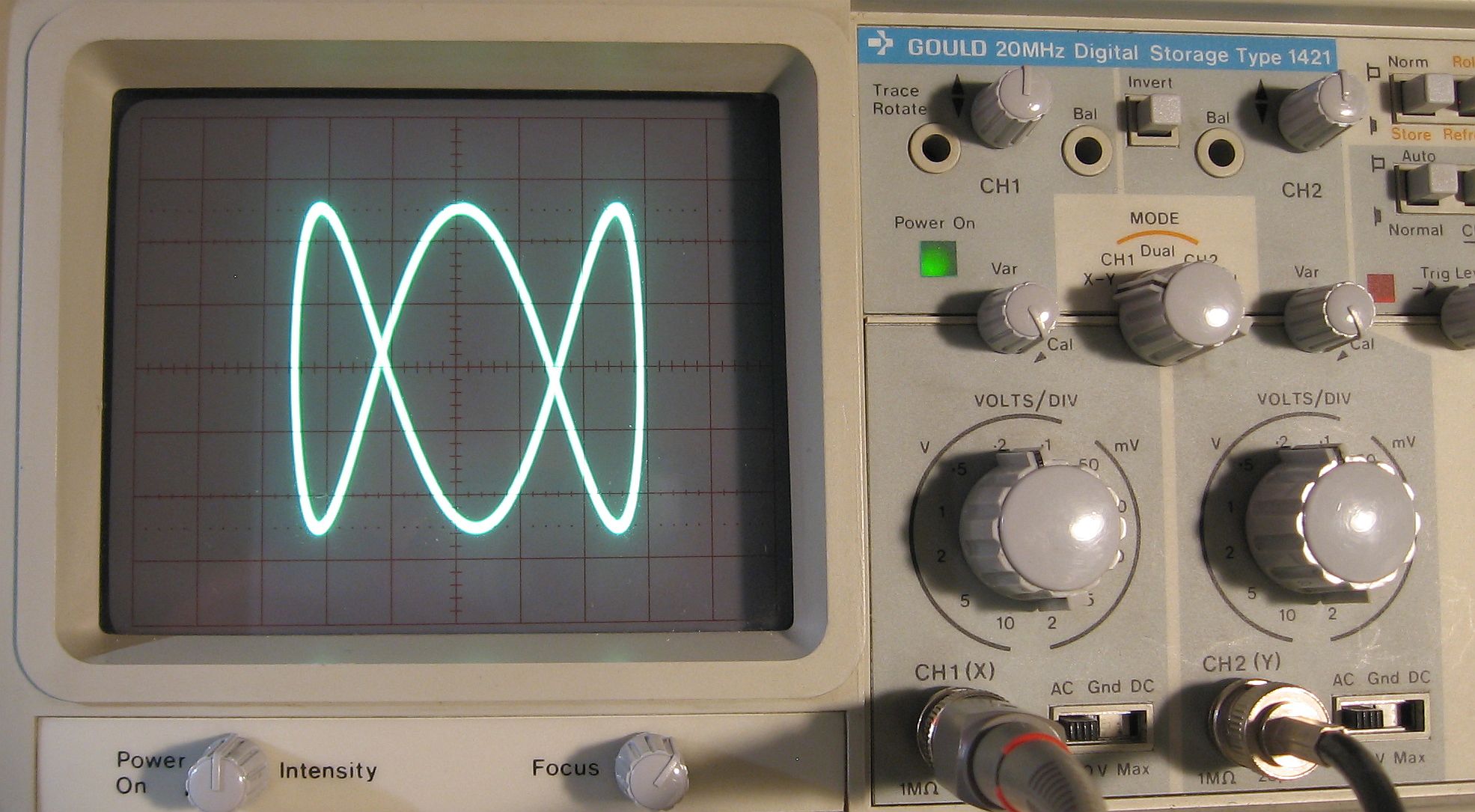
Obiges Video: Frequenzverhältnis nahezu 1:3
Obiges Video: Frequenzverhältnis nahezu 1:4
Obiges Video Frequenzverhältnis nahezu 1:10
Lissajous-Figuren haben in der Laborpraxis kaum eine Bedeutung. Früher dienten sie dazu mit Hilfe eines Vergleichs von Frequenzen Oszillatoren abzugleichen. In alten Industriefilmen, in denen es um Elektronik und Funktechnik ging, zeigte man in den Entwicklungslabors die Lissajous-Figuren gerne, weil sie so schön aussehen. Und das tun sie auch heute noch, weil sie ein zeitlose Reinheit mathematischer Zusammenhänge verkörpern.
