11. März 2015 (umfangreich überarbeitet, fehlende Bilder eingebaut, defekte Links repariert, Design angepasst am 10. November 2023)
Wer seine eigenen Radios und HF-Schaltungen baut oder entwickelt, kommt nicht daran vorbei Spulen, Filter und Schwingkreise selbst zu dimensionieren. Dies geht sowohl mit dem Taschenrechner als auch mit einer Vielzahl von kostenlosen Berechnungsprogrammen. Wie geht das in der Praxis?
Thomsonsche Schwingungsgleichung: Die nachfolgende Formel für die Resonanzfrequenz eines Serien- oder Parallelschwingkreises wird den meisten Lesern sicherlich bekannt sein.
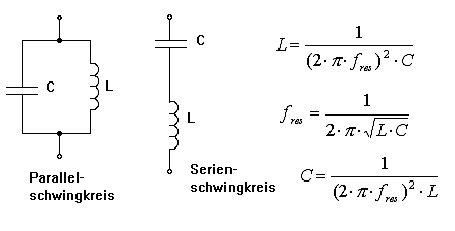
Mit ihr lässt sich die Resonanzfrequenz ausrechnen. Resonanz liegt vor, wenn der Blindwiderstand der Induktivität und der Kapazität des Schwingkreises gleich ist. Der ideale Parallelschwingkreis hat dann einen unendlich hohen Widerstand und der Serienschwingkreis einen unendlich niedrigen Widerstand.
Verluste und Dämpfung in er Praxis: In der Theorie ist das ganz einfach, aber der Praktiker kennt die Tücken. In der Praxis funktioniert der Schwingkreis nicht für beliebige Verhältnisse zwischen der Induktivität (L) und der Kapazität (C). Ein Schwingkreis aus einem 470nF-Kondensator und einem eine kleine Spule aus 3 Windungen mit 3 mm Durchmesser wird keine ausgeprägte Resonanz zeigen. Warum?
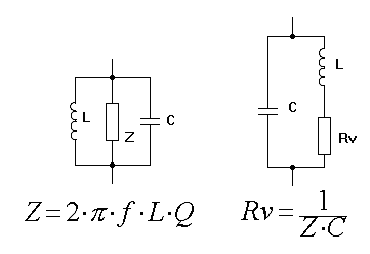
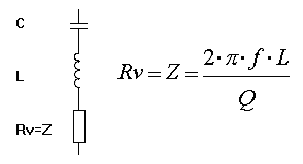
Kondensatoren und Spulen sind nicht ideal. Sie haben Verluste, die wir uns im Ersatzschaltbild als Widerstände parallel oder in Serie vorstellen können. Sie dämpfen den Schwingkreis. Die Verluste der Kondensatoren in einem Schwingkreis sind relativ gering, so dass es meistens ausreicht nur die Spulenverluste zu betrachten. Je weniger Verluste die Spule hat, desto höher ist ihre Güte. Damit hat der Schwingkreis ebenfalls eine besser Güte. Die verlustbehaftete Spule können wir uns als Serienschaltung einer idealen Induktivität und einem Widerstand vorstellen.
Güte, Resonanzfrequenz und Bandreite eines Schwingkreises: Das nachfolgende Bild gilt für den Parallelschwingkreis. Bei der Resonanzfrequenz f liegt an ihm die höchste Spannung an. Er hat dann den höchsten Widerstand. Bei der 0,707-fachen Spannung (0,707 = Kehrwert der Quadratwurzel von 2) liegt die untere (fu) und obere Grenzfrequenz (fo). Der Abstand dieser beiden Grenzfrequenzen fo – fu = b wird Bandbreite B genannt.
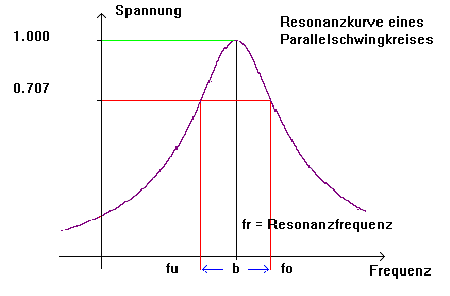
Je größer nun die Bandbreite b bei gleicher Resonanzfrequenz f wird, desto schlechter ist dann der Schwingkreis und desto geringer ist die Güte Q. Nachfolgend der formelmäßig Zusammenhang:
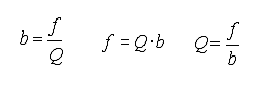
Da die Güte eines Schwingkreises hauptsächlich von der Güte der Spule bestimmt wird, kommt es nun darauf an Spulen hoher Güte einzusetzen. Dabei ist zu beachten, dass die Güte einer Spule von der Frequenz abhängig ist. Je höher die Frequenz, desto höher die Güte der Spule.
Güte einer Spule: Eine reale Spule können wir uns – wie bereits erwänt – aus der Reihenschaltung einer idealen Spule mit der Induktivität L und einem ohmschen Widerstand R vorstellen.
Jede Induktivität L hat nun einen Blindwiderstand XL, der von der Frequenz abhängig ist:
![]()
Je höher nun die Frequenz, desto größer wird natürlich der Blindwiderstand XL. Die Güte Q ist nun der Quotient vom Blindwiderstand XL durch den ohmschen Widerstand R:
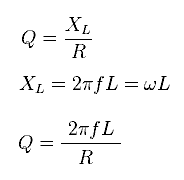
Je kleiner R ist, desto besser ist die Güte der Spule. Deshalb kommt bei Spulen verlustarmes Kernmaterial zum Einsatz. Es werden HF-Litzen verwendet, um den Skineffekt zu senken. Oder die Spulendrähte sind aus dem selben Grund versilbert. Alle Maßnahmen dienen dazu den ohmschen Widerstand R zu senken, um eine möglichst hohe Güte zu erhalten. Der ohmsche Widerstand ist weitgehend konstant. Er wird durch den Skinneffekt mit der Frequenz auch höher, aber nicht in dem Maße, wie der Blindwiderstand ansteigt. Anders kann es aber bei ungeeignetem Kernmaterial aussehen.
Bestimmung der Güte mit einem Rechtecksignal und einem Oszilloskop: Unter http://www.radiomuseum.org … Rechtecksignal.pdf gibt es eine Anleitung.
Was ist der Skineffekt? Mit zunehmender Frequenz haben die Ströme die Tendenz sich mehr außen als innen in einem Leiter zu bewegen. Durch diesen Skineffekt steigt der ohmsche Widerstand. Diesen Effekt nennt man auch Stromverdrängung. Deshalb kommt bei Spulen mit vielen Windungen HF-Litze, die aus vielen einzelnen isolierten Drähten besteht, zum Einsatz. Bei wenigen Windungen wird der relativ dicke Draht versilbert. Es gibt noch andere Erscheinungen, die einen ähnlichen Effekt haben, wenn Windung an Windung dicht an dicht liegen. Leider können wir diese frequenzabhängigen Widerstände, welche durch Stromverdrängung entstehen, nicht mit dem normalen Ohm-Meter erfassen.
Je höher die Induktivität bei gleichem Wirkwiderstand R, desto besser die Güte. Wie aus der unteren der drei vorangegangen Formeln
Q = (2 pi f L) / R
zu erkennen ist, ist die Güte aber auch von der Frequenz abhängig. Wenn wir von der Güte einer Spule sprechen, müssen wir auch die dazugehörige Frequenz nennen. Je höher die Frequenz, desto besser wird die Güte. Eine Spule aus wenigen Windungen Draht hat bei einer Frequenz von 100 MHz eine recht hohe Güte, aber bei 50 Hz ist ihr Blindwiderstand XL = 2 pi L so gering im Vergleich zum Drahtwiderstand, dass wir die Induktivität vernachlässigen können. Der ohmsche Widerstand überwiegt dann. Deshalb verhält sich eine UKW-Spule aus wenigen Windungen dicken Drahtes bei 50 Hz wie ein Stück Draht und nicht wie eine Spule.

Windungszahl, AL-Wert und Induktivität: Je mehr Windungen eine Spule hat, desto höher ist auch ihre Induktivität. Das weiß jeder, der mal eine Spule selbst gewickelt hat. Es kommt noch besser. Die Induktivität steigt mit der Windungszahl quadratisch an. Das erspart uns eine Menge Wickelarbeit. Hat eine Spule bei 100 Windungen 100 µH, dann hat sie bei 200 Windungen bereits 400 µH. der Zusammenhang ist wie folgt:
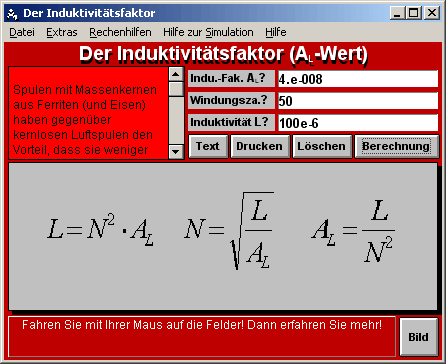
AL-Wert: Mit dem AL-Wert können wir die Anzahl der Windungen mit dem obigen Formelsatz oder Programm berechnen. Kennen wir den AL-Wert nicht, dann wickeln wir 100 Windungen auf den unbekannten Kern, messen die Induktivität und erhalten durch Umrechnung den AL-Wert (AL = L / ( N * N).
Windungszahl und Güte: Der Zusammenhang ist mit zunehmender Windungszahl wie folgt:
1. Die Induktivität L und damit der Blindwiderstand XL steigen mit der Windungszahl im Quadrat.
2. Die ohmschen Verluste durch den Wirkwiderstand R sind von der Drahtlänge oder der Windungszahl abhängig und steigen nur linear an.
Somit erhalten wir nach
Q = XL / R
mit zunehmenden Windungszahlen bessere Güten Q und damit Schwingkreise geringerer Dämpfung. Das ist also der Grund, warum wir so viel wickeln müssen um bessere Güten zu erhalten.
Grenzen der Windungszahl durch Eigenresonanz: Leider bilden die dicht aneinander liegenden Drähte der Wicklungen eine Kapazität, die mit zunehmender Windungszahl steigt. Jede real existierende Spule hat neben dem Ohmschen Wirkwiderstand R oder Rv auch noch eine Kapazität C, die parallel dazu geschaltet ist. Damit bildet eine Spule einen Parallelschwingkreis mit einer Eigenresonanz. Oberhalb dieser Eigenresonanz können wir diese Spule nicht mehr verwenden, da sie dann ihr kapazitive Anteil immer stärker das Verhalten beeinflusst. Wir können also nicht beliebig viele Windungen auflegen, um die Güte eines Schwingkreises für eine bestimmte Frequenz zu verbessern.
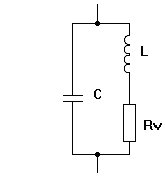
Um die Eigenkapazität einer Spule zu senken, werden die Spulen in Kreuzwickeltechnik gewickelt und in verschiedene Kammern verteilt. Wer einmal eine Spule für Lang- oder Mittelwelle von Hand freihändig gewickelt hat, wird feststellen, dass er wegen der zu großen Eigenkapazität nicht weit genug nach oben in der Frequenz beim Abstimmen kommt.
Berechnungsprogramme für Spulen, Schwinkgreise und HF-Filter:
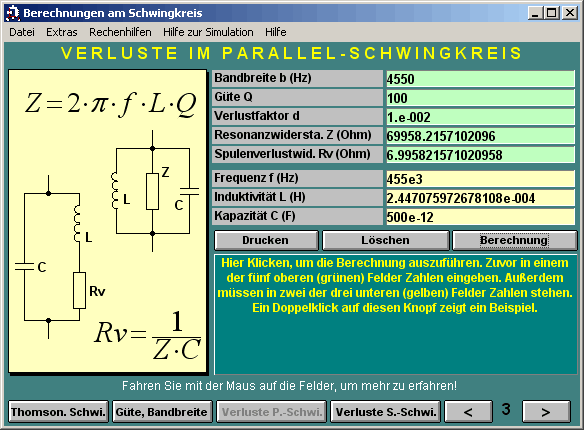
Online-Schwingkreisberechnung: https://goodcalculators.com/resonant-frequency-calculator/
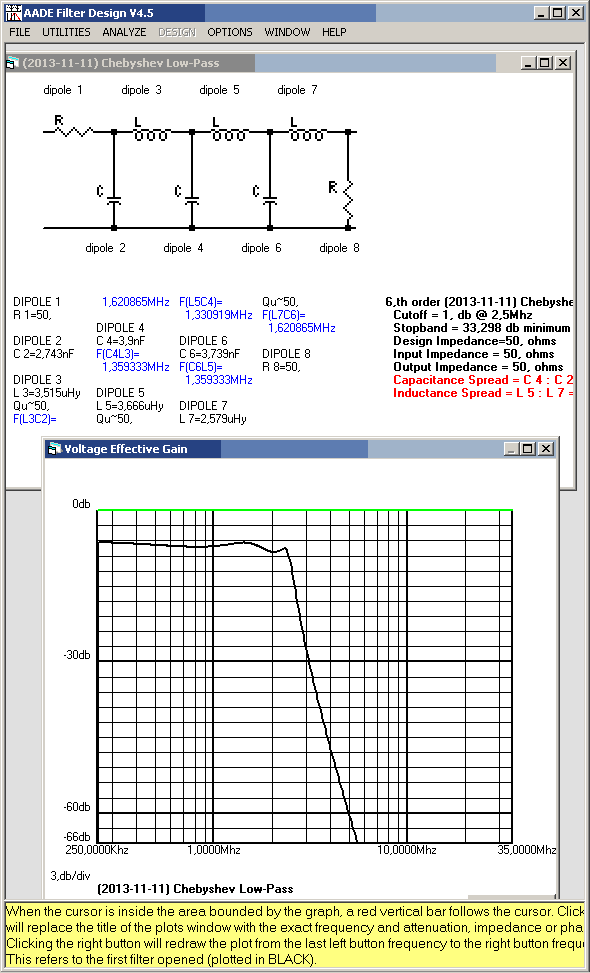

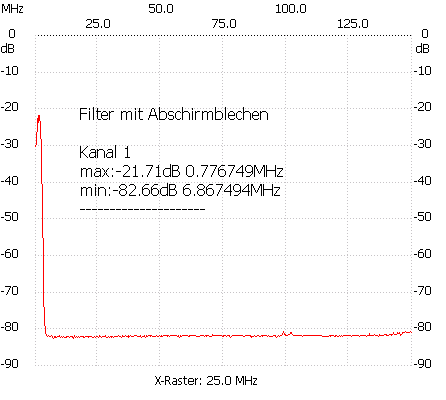
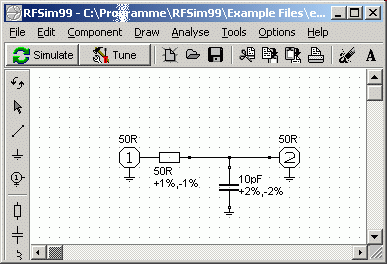
Bauformen von Spulen: