Dreieckgeneratoren liefern einen Spannungsverlauf, der linear ansteigt und abfällt. Dur eine geringfügige Änderung kann ein Sägezahn erzeugt werden.
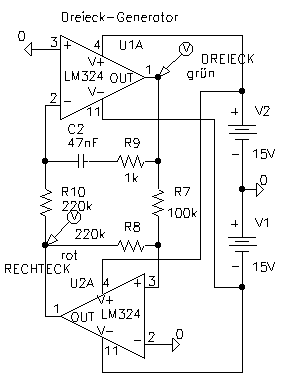
Vollständige Schaltung des Dreieckgenerators
Die Schaltung liefert am Ausgang (Pin1) des oberen Operationsverstärkers (U1A) eine Dreieckspannung (siehe Abbildung unten):
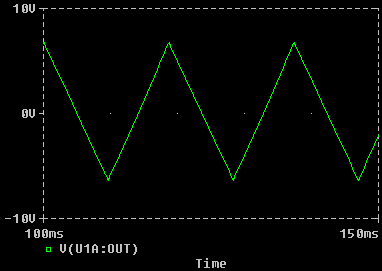
Ausgangsspannung des Dreieckgenerators
Eine Dreieckspannung ist dadurch gekennzeichnet, dass sowohl das Ansteigen wie das Abfallen der Spannung zeitlich linear erfolgt. Die Flanken bilden also auf- und absteigende Geraden.
Nun sei vorweggenommen, dass man (annähernd) lineares An- und Abfallen der Spannung ganz einfach erzeugen kann. Man lädt (entlädt) dazu einen Kondensator über einen relativ hochohmigen Widerstand. Dann steigt (fällt) die Kondensatorspannung proportional zur Zeit. Noch besser ist es, wenn man den hochohmigen Widerstand mit einer Konstantstromquelle lädt.
Die obige Schaltung mag auf den ersten Blick verwirrend aussehen. Sie besteht aber im Prinzip aus zwei bekannten und einfachen Grundschaltungen, die zusammen eine Rückkopplung bilden. Das heißt, der Eingang des einen ist mit dem Ausgang des anderen verbunden:
1. Der untere Operationsverstärker (U2A) ist als Schmitt-Trigger beschaltet. Dies sieht man auf Anhieb daran, weil sich zwischen dem Ausgang (Pin 1) und dem nichtinvertierenden (+) Eingang ein Widerstand befindet. Dieser bildet eine Mitkopplung. Das nachstehende Bild zeigt ausschnittsweise nur den Schmitt-Trigger. Der Eingang des Schmitt-Triggers wird mit dem Dreiecksignal versorgt. Am Ausgang entsteht dann ein Rechtecksignal.
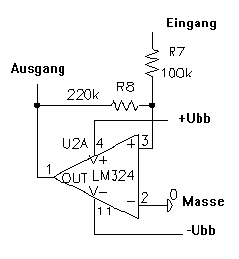
Ausschnitt aus der Schaltung, die einen Schmitt-Trigger darstellt.
Wie diese Schaltung genau funktioniert, ist unter „E1 – Grundschaltungen, Schmitt-Trigger mit OpAmp“ beschrieben. Nachfolgend sind die Formeln wiederholt
Nicht-Invertierender Schmitt-Trigger
Einschaltschwelle:
UEIN = (-R7 / R8) * (-Ubb + 0.1V)
(bei UEIN am Eingang springt die Ausgangsspannung auf +Uaus=+Ubb-0.9 V
Ausschaltschwelle:
UAUS = (-R7 / R8) * (Ubb – 0.9 Volt)
(bei UAUS am Eingang springt die Ausgangsspannung auf -Uaus=-Ubb+0.1 V
Rechnet man nach, ist in unserer Schaltung näherungsweise
UEIN = (-100 / 220) * -14.9 Volt = 6.77 Volt
UAUS = ( -100 / 220) * 14.1 Volt = -6.4 Volt
Je nach Spannung am Eingang (oberer Anschluss von R7) kann der Ausgang des Schmitt-Triggers (Pin 1) nur zwei Zustände einnehmen: Entweder (fast) -Ubb Volt oder (fast) +Ubb. Das nachfolgende Bild zeigt in guter Übereinstimmung mit unserer überschlägigen Berechnung das Dreiecksignal am Eingang (grün) und das Rechtecksignal (rot) am Ausgang.
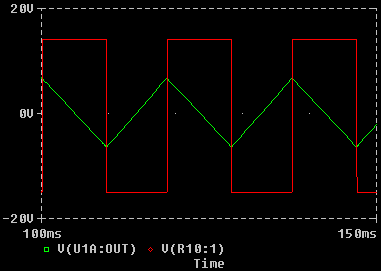
Ein- und Ausgangssignal des Schmitt-Triggers bzw. Aus- und Eingangssignal des Integrators
Nun können wir uns dem anderen Teil der Schaltung widmen:
2. Der obere Operationsverstärker (U1A) ist als „invertierender Verstärker mit Tiefpasswirkung“ beschaltet (Integrator). Er wandelt das Rechtecksignal in ein Dreiecksignal um:
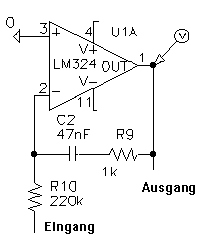
Der obere Teil der Schaltung (Integrator)
R9 soll nur Instabilitäten verhindern. Man benötigt ihn nicht unbedingt. Für die nachfolgenden Überlegungen kann man sich R9 kurzgeschlossen vorstellen.
Angenommen, die Eingangsspannung ist gerade vom negativen Potential auf das positive Potential (ca. +15 Volt) gesprungen. In diesem Moment befindet sich der Ausgang (Pin 1) ebenfalls auf positivem Potential (ca. +6.7 Volt). Da es sich um einen invertierenden Verstärker handelt, „möchte“ die Ausgangsspannung (Pin1) sofort einen negativen Wert annehmen. Doch zuvor muss sich der Kondensator C2 über R10 umladen.
Durch die Gegenkopplung muss sich Pin 2 außerdem immer auf dem selben Potential wie Pin 3 befinden (siehe E1 – Grundlagen, Invertierender Verstärker). Setzt man vereinfachend eine unendliche Verstärkung des Operationsverstärkers voraus, müssen sich Pin 2 und Pin 3 auf Massepotential befinden. Folglich fließt auch
in der kurzen Zeitspanne, in der der Schmitt-Trigger eine positive Spannung liefert, einen konstanten Strom I durch R10:
I = +Ub / R10
I = 15 V / 220 k
I = 0.068 mA
Dieser Strom muss auch durch C2 fließen, da in den Eingang des Operationsverstärkers selbst (praktisch) kein Strom fließt. Die Folge: Der Kondensator lädt sich mit einem (nahezu) konstanten Strom um. Die Spannung am Kondensator ändert sich, so dass sich die Ausgangsspannung stetig Richtung negative Werte bewegt. Nach einer gewissen Zeit ist dieser Wert auf die Ausschaltschwelle des Schmitt-Triggers gesunken. Dadurch wird der Umladevorgang unterbrochen. Die Kondensatorspannung bewegt sich nun in Richtung positiver Werte, bis sich das Spiel wiederholt.
Berechnung der Umladezeiten
Die momentane Kondensatorspannung des C2 entspricht auch der Ausgangsspannung, denn den Kondensator C2 kann man sich parallel zum Ausgang der Schaltung vorstellen. Ein Anschluss des Kondensators liegt am Pin 2 des Operationsverstärkers. Pin 2 liegt immer auf Massepotential. Der andere Anschluss liegt direkt am Ausgang, wenn man R9 vernachlässigt. R9 ist sehr klein im Verhältnis zu R10 und darf deshalb vernachlässigt werden.
Da wir vereinfachend einen konstanten Ladestrom annehmen dürfen (sonst hätten wir ja auch kein Dreiecksignal), brauchen wir nicht wie sonst üblich eine e-Funktion heranziehen, nach der ein Kondensator über einen Widerstand geladen wird. Wir brauchen nur den konstanten Strom kennen, mit dem der Kondensator geladen (entladen) wird. Diesen Strom haben wir bereits ausgerechnet: I = 0.068 mA.
Nun ist die Kapazität C eines Kondensators definiert nach der Formel C = (I * t) / U [C in Farad; I in Ampere; t in Sekunden; U in Volt]. Diese Formel können wir nach t auflösen:
t = (C * U) / I
Wir wissen außerdem, dass sich der Kondensator während eines Umladevorgangs zwischen der Einschaltschwelle UEIN und Ausschaltschwelle UAUS bewegt. Da auch die Kapazität des Kondensators C2 bekannt ist, können wir nun die Zeit t bestimmen, die zwischen den Schaltvorgängen UEIN und UAUS verstreicht.
t = (C * U) / I
t = (C * (UEIN – UAUS) / I
t = (47e-9 F * (6.77 Volt – – 6.4 Volt)) / I
t = (47e-9 F * (13.17 Volt)) / I
t = 6.19e-7 F*V / 0.068e-3 A
t = 9.1e-3 s = 9.1 ms
Eine volle Periode dauert dann 2 * 9.1 ms = 18.2 ms. Der Kehrwert davon ergibt die Frequenz in kHz: 1 / 18.94 ms = 0.052 kHz. Die Schaltung schwingt also mit etwa 55 Hz.
