Ein Schmitt-Trigger kennt am Ausgang nur zwei Schaltzustände. Entweder LOW oder HIGH. Diese hängen von der Eingangsspannung ab.
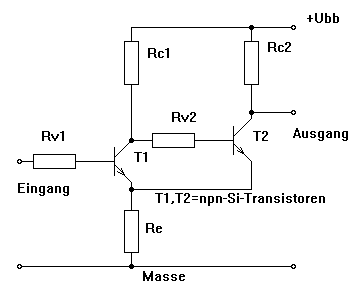
Schmitt-Trigger mit zwei Transistoren.
Schwellwert EIN
Angenommen, die Eingangsspannung würde bei Null Volt beginnend langsam ansteigen, dann erreicht die Eingangsspannung irgendwann den Schwellwert EIN. Ist dieser Pegel erreicht, springt die Ausgangsspannung von LOW auf HIGH.
Schwellwert AUS
Nun sinkt die Spannung und erreicht irgendwann den Schwellwert AUS. Die Ausgangsspannung springt von HIGH auf LOW.
Hysterese
Der Schwellwert EIN liegt immer höher als der Schwellwert AUS. Diese Spannungsdifferenz nennt man Hysterese und hat folgenden Vorteil: Angenommen Schwellwert EIN und Schwellwert AUS würden auf gleichem Potential liegen und die Eingangsspannung hätte zufälligerweise ebenfalls dieses Potential. Kleinste Schwankungen der Eingangsspannung würden dann zum Hin- und Herkippen des Ausgangs führen. Unter Umständen gerät die Schaltung ins Schwingen.
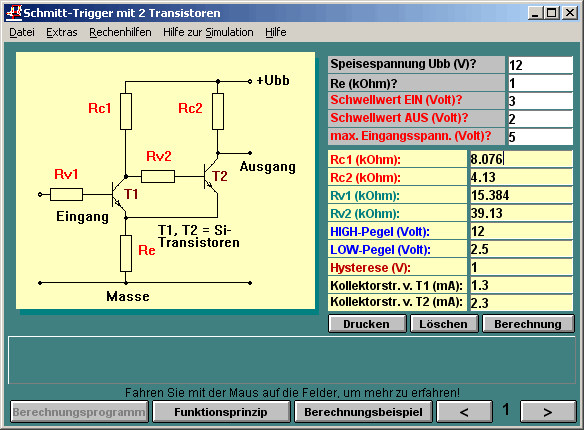
Berechnungsprogramm zum Schmitttrigger mit zwei Transistoren, welches es hier in der E1 gibt.
Anwendung
Schmitt-Trigger wandeln eine analoge, schwankende Spannung in ein digitales Signal um. So wird zum Beispiel eine Sinus-Schwingung am Eingang zu einem Rechteck-Signal am Ausgang.
Berechnung
Bei der Berechnung kann man zur Vereinfachung die Basisströme vernachlässigen.
1. Zustand: T1 gesperrt, T2 leitend
Der Ausgang befindet sich im LOW-Zustand. Es fließt durch T1 und Rc1 kein Strom.
Durch Rc2 ,T2 und Re muss dann jeweils ein Strom von gleicher Höhe fließen (der Basisstrom ist vernachlässigbar klein). Diesen Strom Ic2 können wir leicht bestimmen:
Ubb – Ucesat
Ic2 = ——————————-
Re + Rc2
Da wir nun Ic2 kennen, können wir den Spannungsabfall an Re bestimmen:
URe = Re • Ic2
Nun können wir den LOW-Pegel des Ausgangs bestimmen:
ULow = URe + Ucesat
ULow = URe + 0.2 Volt
Weiter können wir die Einschaltschwelle UEIN berechnen:
UEIN = URe + Ube
UEIN = URe + 0.7 Volt
2. Zustand: T1 leitend, T2 gesperrt
Um sich diesen Zustand besser vorstellen zu können, entfernt man den Transistor T2. Am durchgesteuerten Transistor T1 fällt Ucesat = 0.2 Volt ab.
Durch Rc1 und Re fließt der gleiche Strom, und an der Reihenschaltung dieser beiden Widerstände fällt die Spannung Ubb-Ucesat ab (vergleiche 1. Zustand, T2). Ic1 berechnet sich zu:
Ubb – Ucesat
Ic1 = —————————
Re + Rc1
Da wir nun Ic1 kennen, können wir den Spannungsabfall an Re berechnen:
URe = Re • Ic1
Jetzt können wir (nach dem gleichen Prinzip wie beim 1. Zustand) den Schwellwert AUS berechnen:
UAUS = URe + Ube
Praktische Berechnung, wenn Ubb, Re, UAUS und UEIN gegeben sind:
Durch Umformung erhält man folgende Formeln (verwendet im Berechnungsprogramm E1):
Rc1=(((Ubb – 0.2 V) / (UAUS – 0.7 V))-1)•Re Kollektorwiderstand v. T1 (kOhm)
Rc2=(((Ubb – 0.2 V) / (UEIN – 0.7 V))-1)•Re Kollektorwiderstand v. T2 (kOhm)
Ic1=(Ubb – 0.2) / (Rc1+Re) Kollektorstrom v. T1 (mA)
Ic2=(Ubb – 0.2) / (Rc2+Re) Kollektorstrom v. T2 (mA)
ULOW=(Re•Ic2)+0.2 V LOW-Pegel am Ausgang (Volt)
UHIGH=Ubb HIGH-Pegel am Ausgang (Volt)
Umax = max. Eingangsspannung in Volt, Übersteuerungsfaktor = 3, ß1=min. Strom-
verstärkungsfaktor von T1, ß2= min. Stromverstärkungsfaktor v. T2, ü=3 bis 10 (Übersteuerungsfaktor.
Rb1=(((Umax-(Re•Ic2)-Ube))•ß1)/(ü•Ic1) Basisvorwiderstand von T1
Rb2=(Ubb-(Re•Ic2)-Ube)/(ü•(Ic2/ß2)) Basisvorwiderstand von T2
(Alle Werte in mA, kOhm und Volt)
