Das dB (Dezibel) wird in der Akustik und Nachrichtentechnik verwendet, um Spannungs- und Leistungverhältnisse zu beschreiben. Der ursprüngliche Grund dafür ist, dass das die Empfindlichkeit des menschlichen Ohres logarithmisch gestaltet ist. Eine Verdoppelung der Leistung eines Verstärkers entspricht zum Beispiel einem Gewinn von 3 dB. Bei gleichen Eingang- und Ausgangsimpedanzen entspricht dies einer Spannungsverstärkung von etwa 1,413. Bei Angaben von dB entfällt also die Angabe, ob es sich um ein Verhältnis von von Leistungen oder Spannungen handelt.
A. Leistungs-Verstärkung: Das Verhältnis Ausgangs-Leistung (Paus) zu Eingangs-Leistung (Pein) bezeichnet man als Leistungs-Verstärkung.
1. Beispiel: Eine Verstärkerbaugruppe liefert eine Ausgangs-Leistung von 20 Watt (Paus), wenn dazu an seinem Eingang eine Leistung von 1 Watt (Pein) geliefert werden muss. Die Leistung wird dann um den Faktor Paus / Pein = 20 / 1 = 20 verstärkt.
2. Beispiel: Ein Dämpfungs-Glied soll bei einer Eingangs-Leistung (Pein) von 10 Watt eine Ausgangs-Leistung von 2.5 Watt liefern. Der Leistungsverstärkungs-Faktor würde dann Paus / Pein = 2.5 / 10 = 0.25 betragen. Da er kleiner als 1 ist, liegt eine Dämpfung vor.
Multiplikation der Leistungs-Verstärkungsfaktoren: Den Verstärker aus dem ersten Beispiel und das Dämpfungs-Glied aus dem zweiten Beispiel können wir in Reihe schalten. Die gesamte Verstärkung dieser Anordnung erhalten wir, wenn wir die einzelnen Verstärkungsfaktoren multiplizieren. In unserem Falle wären dies
20 · 0.25 = 5.
Das Dezibel (dB): Leistungsfaktoren werden oft in Dezibel (dB) angeführt. Dazu wird folgende Formel verwendet:
g=10·lg(Paus/Pein).
In andererer Darstellung und mit den Umformungen nach Paus (Ausgangsleistung) und Pein (Eingangsleistung):
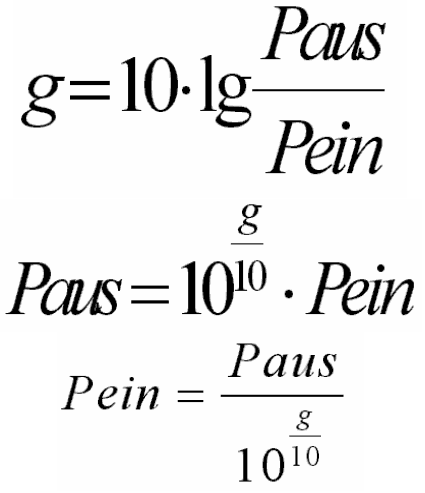
Umrechnungen von dB und Leistungsverhältnissen.
Darin bedeutet lg der Logarithmus zur Basis 10. Auf Taschenrechnern wird er oft fälschlicherweise mit log abgekürzt.

Der Logarithmus zur Basis 10 wird auf Taschenrechnern fälschlicherweise mit „log“ abgebkürzt.
Weniger gebräuchlich ist das Rechnen mit Bel. 1 Bel = 10 dB. Die Formel dazu lautet:
g=lg(Paus/Pein).
Das Rechnen mit dB-Angaben hat zwei Vorteile:
1. Die Zahlenangaben werden durch die logarithmische Darstellung nicht so groß: So entsprechen 20 dB einem Faktor von 100. 30 db entsprechen einem Faktor von 1000. Anmerkung: 3 dB entsprechen einer Leistungsverdoppelung, 6 dB einer Vervierfachung der Leistung. Diese markanten Werte sollte man sich merken.
2. Addition von db-Angaben: Die Leistungs-Verstärkungs-Angaben mussten wir in unserem Beispiel multiplizieren. Wenn wir mit dB rechnen, müssen wir die dB-Werte nur addieren. Sie können dies nachprüfen, indem Sie die beiden Faktoren 20 und 0.25 in dB-Werte umrechnen und addieren:
13 dB – 6 dB = 7dB.
7dB entspricht aber einem Leistungs-Verstärkungsfaktor von 5, wie die Gegenprobe zeigt.
Dämpfung: Leistungsverstärkungs-Faktoren unter 1 nennt man Dämpfungen, weil ja in diesem Fall das Signal nicht verstärkt sondern abgeschwächt wird. Dämpungen drücken sich dann als negative dB-Werte aus. Ein Sonderfall ist die Verstärkung mit dem Faktor 1. Dies bedeutet, dass die Eingangsleistung gleich der Ausgangsleistung ist und entspricht einer Verstärkung von 0 dB.
Pegel – dBm: Leistungsverhältnisse und dB geben nur Auskunft über das Verhältnis zweier Werte. Den tatsächlichen Wert in Volt, Ampere oder Watt kennt man dadurch aber nicht.
Mit Pegel-Angaben kann man aber den tatsächlichen Wert in Watt (oder mW) ermitteln. Dazu muss man sich für Pein auf einen festen Bezugswert einigen.
dBm: Bei der Angabe in dBm geht man davon aus, dass Pein = 1mW beträgt. Beispiel: Wir messen, dass ein Verstärker eine Leistung von 3 dBm liefert. Das entspricht einer Leistung von 2 mW. Dazu müssen wir in dem hier vorliegenden Berechnungs-Programm (dbp.exe) unter Pein eine 1 für 1 mW eintragen und unter g eine 3 für 3 dBm einsetzen. Unter Paus erhalten wir dann das Ergebnis in mW. Das dbm bezieht sich in der Akustik auf 600 Ohm Impedanz und in der HF-Technik auf meistens 50 Ohm.
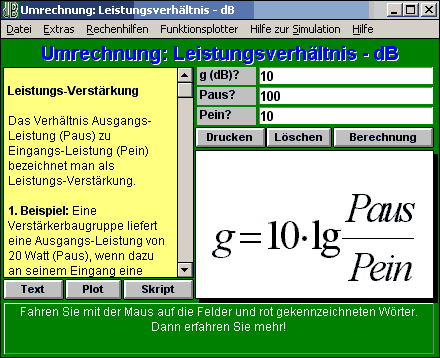
Berechnungsprogramm zur Umrechnung von Leistungsverhältnissen aus „E1 – Das interaktive Elektronikprogramm„.
Nehmen wir als Bezugswert 1 Watt erhalten wir dBW, bei picoWatt erhalten wir dBpW.
Rechentipps: Bestimmte Programmier-Sprachen (z.B. Basic) und Taschenrechner kennen nur den natürlichen Logarithmus ln. Man kann sich behelfen, indem man folgende Formel verwendet:
g=M · 10 · ln(Paus/Pein)
mit M=lg(e)=0.43429448 … .
Dabei ist e=2.7182818 … die eulersche Zahl.
Das Plot-Programm WGNUPLOT kennt nur den natürlichen Logarithmus und kürzt LN mit LOG ab.
Überschlagsrechnen: Wenn Sie sich merken, dass 3 dB Leistungsverdopplung und 6 dB Leistungs-Vervierfachung bedeutet, können Sie leicht andere Werte im Kopf ermitteln. Zum Beispiel sind dann 3 dB + 6 dB = 9 dB. Dies ist auch die Multiplikation der entstrechenden Faktoren 2 und 4. 9 dB entsprechen also dem Faktor 2 · 4 = 8.
Außerdem sind die Leistungsverhältnisse für 10 dB, 20 dB, 30 dB u.s.w. leicht zu merken:
10 dB = 10-fache Verstärkung
20 dB = 100-fache Verstärkung
30 dB = 1000-fache Verstärkung
Beispiel: Eine Antenne hat einen Gewinn von 17 dB gegenüber einen Dipol. Das sind 20 dB – 3 dB. Also Faktor 100 / Faktor 2 = 50.
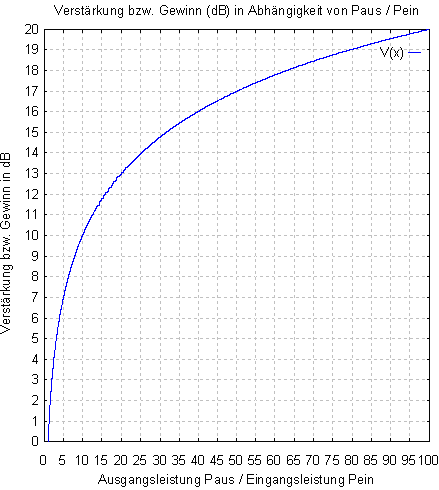
Grafik über das Verhältnis zwischen Gewinn in dB und Leistungsverstärkung.
B. Spannungs-Verstärkung: Das Verhältnis Ausgangs-Spannung (Uaus) zu Eingangs-Spannung (Uein) bezeichnet man als Spannungs-Verstärkung.
Spannungs-Verstärkungen kann man ebenso wie die Leistungs-Verstärkung in dB angeben. Die Formel lautet:
g=20·lg(Uaus/Uein).
Oder „schöner“ geschrieben:
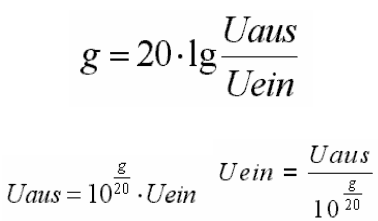
db-Berechnungen bei Spannungsverhältnissen.
Auffallend ist, dass hier im Gegensatz zur Formel für die Leistungs-Verstärkung mit dem Faktor 20 anstatt dem Faktor 10 gearbeitet wird.
Dies hat den großen Vorteil, dass wir bei dB-Angaben nicht wissen müssen, ob es sich um Spannungs- oder Leistungsverhältnisse handelt.
Sagt jemand, ein Signal wurde „um 6 dB verstärkt“, können wir sowohl die Spannungs- als auch die Leistungsverstärkung ermitteln.
Für das Leistungs-Verhältnis verwendet man die Formel
g=10·lg(Uaus/Uein)
und für das Spannungs-Verhältnis mit der Formel
g=20·lg(Paus/Pein).
Warum ist das so? Ersetzt man Paus und Pein durch P=U·U/R erhält man für
Paus Uaus·Uaus·Rein
——— = ————————–
Pein Uein·Uein·Raus
Paus Uaus2·Rein
——— = ——————-
Pein Uein2·Raus
Geht man davon aus, dass Rein = Raus ist, kürzen sich die Widerstände heraus und man erhält:
Paus
——— = (Uaus / Uein)2
Pein
und damit
g=10·lg(Uaus / Uein)2
Nach den Rechenregeln für Logarithmen erhalten wir dann:
g=2·10·lg(Uaus / Uein)
g=20·lg(Uaus / Uein)
Um diese Formel anwenden zu können, ist es wichtig, dass die Spannungen Uaus und Uein an gleichen Widerstandswerten gemessen werden.
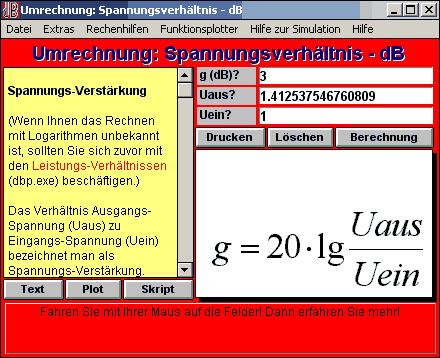
Berechnungsprogramm zur Umrechnung von Spannungsverhältnissen aus „E1 – Das interaktive Elektronikprogramm„.
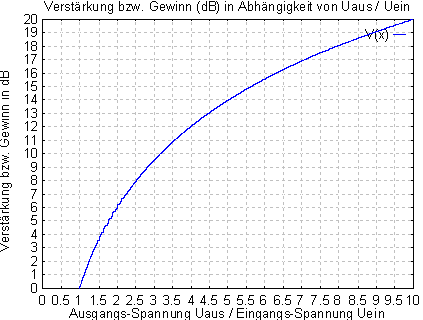
Spannungsverhältnisse und dazugeörige Werte in dB.
Pegel: Wie bei den Leistungs-Verhältnissen kann man bei den Spannungs-Verhältnissen ebenfalls mit Pegeln arbeiten, wenn man neben Uein als Bezugswert auch einen Widerstandswert angibt. Bei Leistungspegeln hingegen braucht man den Widerstand nicht zu definieren.
dBu: 0 dBu sind definiert bei einer Spannung von 0.775 V an einem Widerstand mit Raus=Rein=600 Ohm. Wenn Sie nachrechnen, werden Sie feststellen, dass bei diesen Bedingungen an Rein bzw. Raus eine Leistung von 1 mW anfällt. Damit ist dBu mit dBm identisch, weil 0 dBm ebenfalls bei 1mW definiert ist.
dBµV: In der Fernsehtechnik ist dBµV gebräuchlich. Dabei wird als 0 dBµV eine Spannung von 1µV an 75 Ohm definiert.
Online-Umrechnungsprogramm für dBm und db: http://www.daycounter.com/Calculators/Decibels-Calculator.phtml
