Mit Schwingquarzen lassen sich steilflankige Bandfilter mit Filterbandbreiten realisieren, die für CW, SSB und AM geeignet sind. Am Beispiel eines AM-Filters mit 6 Quarzen und einer Zwischenfrequenz von 10 MHz möchte ich die Vorgehensweise kurz demonstrieren.
Worauf es bei der Vorgehensweise ankommt: Für die Berechnung der Quarzladderfilter gibt es verschiedene Programme. Das Programm „Dishal“ von DJ6EV zum Beispiel verwendet das Rechenverfahren nach Dishal. Für die Berechnung werden die Werte des Quarzersatzschaltbildes verlangt. Alle Quarzexemplare des Filters sollten eng toleriert sein. Nun unterliegen die Quarzdaten Exemplarstreuungen. Alle Quarze müssen deshalb vorher ausgemessen werden. Quarzeexemplare, die untereinander wenig abweichen, müssen dann ausgesucht werden. Die eigentliche Arbeit steckt in Suche der passenden Quarzexemplare.
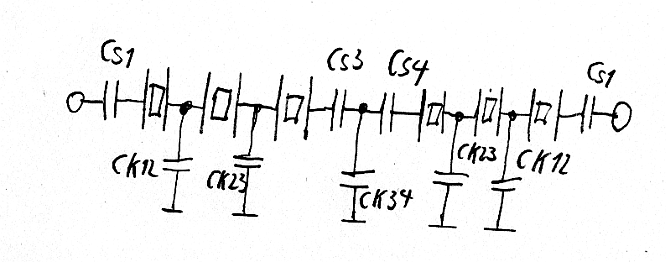
Schaltbild eines 6-poligen Quarzladderfilters. Mit dem Programm Dishal werden die Kapazitätswerte und die Impedanzen berechnet. Doch vorher müssen die Quarze einzeln ausgemessen werden.

Versuchsaufbau eines Quarzladderfilters. Wichtig ist die große Massefläche für eine gute Sperrdämpfung. Die langen Beinchen der Bauteile haben kaum Einfluss auf die Fitereigenschaften. Bei den langen Quarzgehäusen sind Wäscheklammern für die vorübergehende Befestigung der Quarze sehr praktisch.
Wahl der Zwischenfrequenz (ZF) und damit der Quarzfrequenz: Die ZF sollte nicht auf einem Rundfunkband liegen, weil dann die starken Rundfunkbänder durschschlagen können. Je höher die ZF, desto breiter können die Filterkurven gestaltet werden. Für den AM-Rundfunk werden mindestens 7 kHz Bandbreite für einen guten Klang benötigt. Die maximale Bandbreite kann faustformelmäßig mit (Quarzfrequenz / 1000) * 0,8 bestimmt werden. Das wären bei 10 MHz dann 8 kHz Bandbreite. Mit Kompensationsmethoden sind noch breitere Filter möglich.
Wahl der Quarze: Es gibt Quarze in hoher Bauform (Standardquarze) und niedriger Gehäusebauform (low profile). Ich würde denen im hohen Gehäuse den Vorzug geben. Mit ihnen lassen sich Filter besser konstruieren. Sie haben eine kleinere Serieninduktivität und nach meiner Erfahrung bei breiten Filtern eine höhere Flankensteilheit auf der linken Seite.

Viele Quarze werden benötigt. In der Hand halte ich 200 Stück. Hier sind es low profile-Typen, die eigentlich nicht so geeignet sind, doch der sehr günstige Preis eines chinesischen Händlers war verlockend.
Wahl der Anzahl der Quarze im Filter: Je höher die Anzahl der Quarze, desto steilflankiger wird das Filter im Idealfall. Allerdings wird das Ausmessen und Auswählen der eng tolerierten Quarzexemplare immer schwieriger, wodurch der Erfolg vereitelt wird. Man beginne mit einem Filter aus 4 bis maximal 6 Quarzen. Je schmalbandiger es sein soll, desto leichter fällt die Aufgabe.
Ausmessen der Quarze für die Ermittlung der Quarzparameter: Es werden Quarze benötigt, die eine Toleranz der Serienfrequenz fs von plus minus 1% der gewünschten Bandbreite haben. Bei 7 kHz Bandbreite darf also die Serienresonanz der Quarze untereinander maximal 140 Hz abweichen. Die Serien-Induktivität Lm soll maximal nur um 1,5% abweichen. Um 6 passende Quarze zu finden, müssen nach meiner Erfahrung mindestens 30 Quarze ausgemessen werden. Alle Quarze sollten natürlich aus der gleichen Produktion stammen.
Die Verschiedenen Methoden des Ausmessens sind unter
http://www.cliftonlaboratories.com/Documents/Crystal%20Motional%20Parameters.pdf
beschrieben.
Da ich den Netzwerktester des FUNKAMATEUR (FA-NWT) besitze, habe ich mich für die Methode nach
http://www.giangrandi.ch/electronics/crystalfilters/xtaltest.html
entschieden, weil dort auch gleich ein Berechnungsprogramm online mitgeliefert ist, das die Quarzparameter ermittelt. Den dort vorgeschlagenen Messaufbau musste ich allerdings verändern und mit Dämpfungsgliedern versehen, da vor allen Dingen die Pegel zu hoch sind, was zu Messfehlern führt. Bei jeder neuen Messung am gleichen Quarz kommen dann andere Werte heraus. Das Problem habe ich noch nicht vollständig gelöst. Wenn eine sehr hohe Dämpfung am Eingang benötigt wird, muss das Signal hinter dem Quarz verstärkt werden, um noch die Parallelresonanz messen zu können. Es ist immer mit der maximalen Anzahl von Messpunkten und somit mit der kleinsten Schrittweite zu arbeiten.
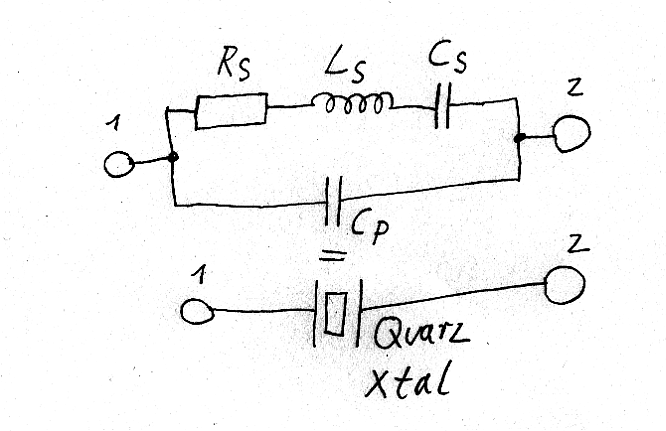
Das vereinfachte Quarzersatzschaltbild. Abgesehen von Rs, welches für die Quarzgüte verantwortlich ist, sind die übrigen Werte zu ermitteln. Rs kann mit guter Näherung mit 6 Ohm angenommen werden, falls Quarzmodelle für Simulationsprogramme wie Spice oder PSpice benötigt werden.
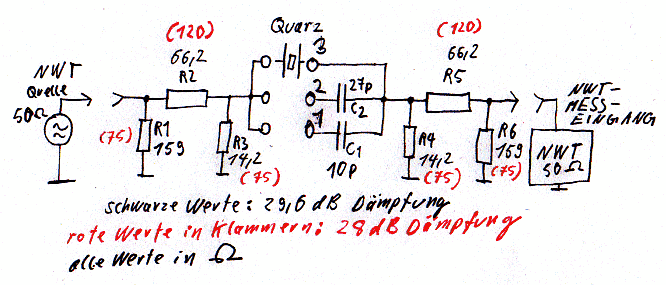
Geeignete Messschaltung mit Dämpfungsgliedern für die Anpassung. Die schwarzen Werte sind nach DIN. Die beiden Ziehkondensatoren können für bestimmte Messverfahren notwendig sein. Beim FA-NWT sind eventuell weitere Dämpfungsglieder am Eingang notwendig. Dann muss das Ausgangssignal unter Umständen mit einem Verstärker angehoben werden. Wird nämlich mit zu hohen Pegeln gemessen, schwanken die Messwerte bei einem einzigen Exemplar durch „Überlastung“ des Quarzes.

Aufbau des Messadpters, der noch bis 10 MHz brauchbare Ergebnisse liefert. Auf der Unterseite sind die Widerstände und Kondensatoren eingelötet.
Wer keinen FA-NWT besitzt, kann mit einem Messsender und einem Frequenzzähler mit 1 Hz Auflösung arbeiten. Richtig elegant geht es mit einem VNWA.
Selbstverständlich sind die Quarze vor der Messung mit Nummern zu beschriften. Der Messsender sollte eine Weile warm gelaufen sein und die Quarze werden, wenn man es ganz genau machen will, mit einer Holzwäscheklammer hantiert, um eine Erwärmung durch die Finger zu vermeiden.
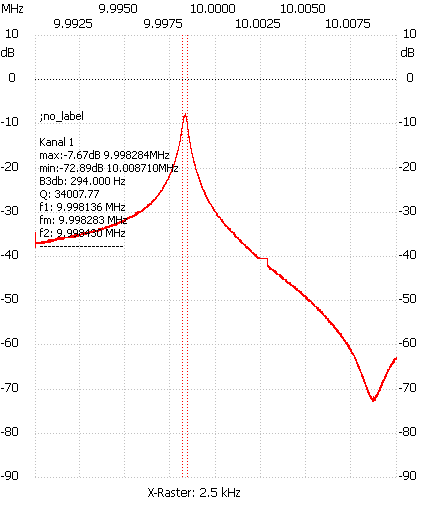
Aufnahme der Serienresonanzfrequenz (links) und Parallelresonanzfrequenz (rechts) mit dem FA-NWT. Hier noch ohne Dämpfungsglieder, nicht normgerechter Anpassung und zu hohem Pegel.
Auswahl der gemessenen Quarze: Alle Quarzparameter werden in ein Formblatt eingetragen. Dann geht es an die Auswahl der Quarze, um in diesem Beispiel diejenigen 6 Quarze mit den geringsten Abweichungen untereinander zu finden. Dabei ist nicht nur auf die Serienresonanzfrequenz zu achten, sondern auch auf die Serieninduktivität. Selbstverständlich sind die Quarze vor der Messung mit Nummern zu beschriften.
Das Berechnungsprogramm Dishal von DJ6EV: DK7JB hat unter
http://www.bartelsos.de/dk7jb.php/quarzfilter-horst-dj6ev
sehr viel Literatur, Platinenentwürfe und das kostenlose Programm Dishal zur Verfügung gestellt. Das Programm und weitere Literatur sind auch unter
http://fa-nwt.akadns.de/blogs/blog4.php
zu finden.
Berechnungen mit dem Windows-Programm Dishal: Das Programm ist eigentlich selbsterklärend. Nach dem Entpacken der Zip-Datei kommen neben der EXE-Datei, die nicht installiert werden muss, noch zwei PDF-Dateien zum Vorschein, welche die Bedienung jeweils in Deutsch oder Englisch erklären.
Um mit der Berechnung starten zu können, ist entweder die Serien-Induktivität Lm (Ls) oder die Parallel-Kapazität Cm (Cs) des Quarzersatzschaltbildes einzutragen. Dann ist noch die Serien-Resonanzfrequenz fs (in kHz, nicht MHz) einzutragen und die Parallelkapazität des Cp des Quarzersatzschaltbildes. Die Quarzgüte oder Rs wird nicht verlangt. Das Programm nimmt verlustfreie Quarze an.
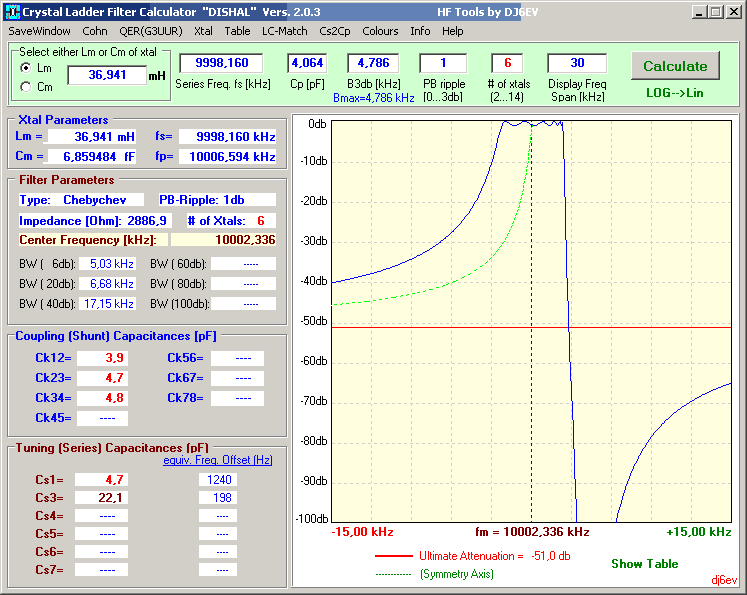
Berechnung des 6-poligen Filters mit Hilfe der gemessenen Quarzdaten. Wir tragen die Daten eines Quarzes ein, dessen Werte im Durchschnitt der eingesetzten Quarze liegen.
Nun können wir die gewünschten Filtereigenschaften eingeben und mit dem Programm „herumspielen“. Ausgegeben werden die Kapazitätswerte und die Eingangs- und Ausgangsimpedanzen, welche für eine korrekte Anpassung notwendig sind, auf der linken Seite des Programm. Das dazugehörige Schaltbild finden wir auf den letzten Seiten der beigefügten Hilfe.
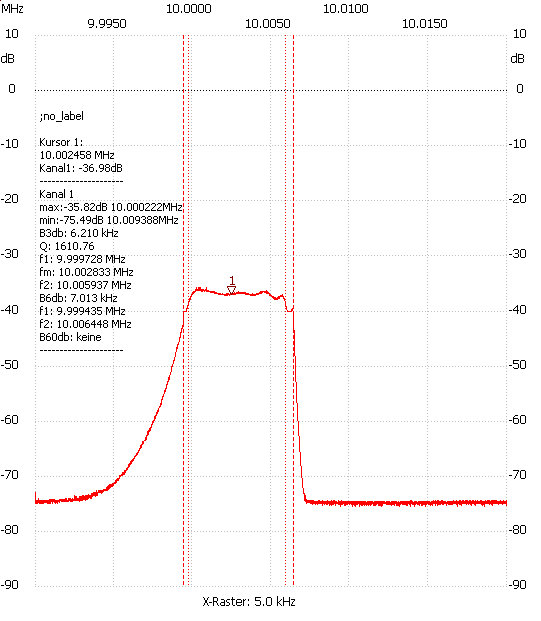
Die tatsächliche Filterkurve. Für die Anfang nicht schlecht. Durch die logarithmische Darstellung wirkt die Filterkurve abgeflachter als sie tatsächlich ist. Dass die linke Seite flacher ausfällt ist normal. Als Kondensatoren wurden nur 5pF- und 22pF-Werte eingesetzt. Dadurch erklärt sich die Dachschräge. Die hohe Einfügedämpfung erklärt sich durch die beiden 2,8-kOhm-Widerstände für die Anpassung des Ein- und Ausgangs. Der FA-NWT arbeitet mit 50 Ohm an seinem Ein- und Ausgang. Mehr als -75 dB Sperrdämpfung kann mein FA-NWT nicht anzeigen. Mit Übertragern zur Anpassung sähe man die wirkliche Sperrdämpfung des Filters.

Nahaufnahme des tatsächlichen Aufbaus.
Messung des realen Filters: Die Wahrheit kommt zu Tage, wenn wir das Filter aufbauen und durchmessen. Meistens fällt es etwas breiter und welliger als erwartet aus. Die Welligkeit können wir durch die Impedanzanpassung noch minimieren. Das Programm bietet unter anderem noch die Möglichkeit Ziehkondensatoren zu berechnen, um Unterschiede der Quarzexemplare auszugleichen.
Alternative Messung der Quarz-Parameter mit dem Programm von DJ6EV: Das Programm ist für den FA-NWT geschrieben worden und unter http://fa-nwt.akadns.de/blogs/blog4.php in der Zip-Datei zu finden. Eine Installation ist nicht notwendig. Es berechnet mit einer einzigen Messung nach der 3-dB-Methode alle erforderlilchen Quarzparamter automatisch. Nur die Parallelkapazität Cp des Quarzes muss mit einem L/C-Meter ermittelt werden. Eine Anleitung liegt bei. Somit geht es mit diesem Programm noch bequemer.
Quarze mit dem FA-NWT und einem Messadapter ausmessen: Eine weitere sehr gute Anleitung für das Ausmessen von Quarzen mit dem FA-NWT befindet sich auf
https://dl6gl.de/selbstbau-trx/2-der-rx-signalpfad/2-4-quarzfilter-selber-bauen-kein-problem.html.
Es wird dort ein Messadapter vorgestellt, welcher neben der Impedanz-Anpassung durch Dämpfungsglieder einen nachgeschalteten MMIC zur Pegelanhebung verwendet. In Verbindung mit der linearen Messsonde des FA-NWT erhöht dies die Messgenauigkeit wesentlich.
