Lädt man einen Kondensator mit einem konstanten Strom auf, steigt an diesem Kondensator die Ladespannung linear an. Auf diesem Prinzip basieren viele Sägezahngeneratoren, so auch jene mit dem NE 555.
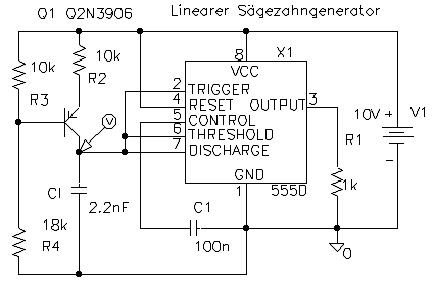
Schaltbild des Sägezahngenerators mit einem NE555. Der Sägezahn ist am Kollektor des Q1. Der Ausgang am Pin 3 des NE555 liefert ein Rechteck.
Der pnp-Transistor Q1 (in der angelsächsischen Literatur werden Transistoren mit Q und nicht mit T abgekürzt) gibt an seinem Kollektor einen konstanten Strom ab, welcher den Kondensator Cl auflädt. Dadurch steigt die Spannung am Kollektor linear an, bis der Timerbaustein den Kondensator Cl schlagartig entlädt. Diese Entladung geschieht, wenn 2/3 der Speisespannung erreicht sind. Beendet wird der Entladevorgang, wenn die Spannung am Kondensator auf 0 Volt abgesunken ist und der Kondensator vollständig entladen ist. Die Sägezahnspannung wird am Kondensator Cl abgenommen.
Berechnung des Konstantstroms: Dazu müssen wir uns überlegen, welche Spannung am Widerstand R2 abfällt. Diese finden wir schnell heraus, wenn wir die Spannung an R3 kennen und von ihr die Schwellenspannung (Basis-Emitterspannung) in Höhe von 0.7 Volt abziehen. Den Spannungsabfall an R3 können wir einfach berechnen, wenn wir R3 und R4 als einen unbelasteten Spannungsteiler betrachten.
Die Spannung an R3 kann man nach folgender Verhältnisgleichung ermitteln:
R3 / ( R3 + R4) = x Volt / 10 Volt
Nach einer Dreisatzrechnung mit dem fallen an R3 ca. 3.6 Volt ab:
(10k / ( 10k + 18k)) * 10 Volt = 3,6 Volt
Dann müssen an R2 3.6 Volt – 0.7 Volt = 2.9 Volt abfallen. R2 hat einen Wert von 10 kOhm. Folglich fließen nach dem ohmschen Gesetz I = U / R = 2.9 Volt / 10 kOhm = 0.29 mA durch den Emitter und damit überschlägig auch durch den Kollektor des Transistors. Diese 0.29 mA hat der Konstantstrom, der den Kondensator auflädt.
Ladezeit des Kondensators: Die Lagezeit t des Kondensators entspricht der Anstiegszeit des Sägezahnsignals. Sie berechnet sich mit der Formel
t = (C·U) / I (mit t in sec, C in Farad, U in Volt und I in Ampere).
Um t zu erhalten, müssen wir für C den Wert von Cl einsetzen ( 2.2nF = 2.2e-9 Farad), für I setzen wir den Konstantstrom von 0.29 mA = 0.29e-3 A ein.
Da sich der Kondensator wie schon gesagt auf 2/3 = 0.666 der Speisespannung (10 Volt) auflädt ist
U = 10 Volt · 0.66 = 6.6 Volt.
Diese Werte setzen wir nun ein:
t = (C·U) / I
t = ( 2.2e-9 F · 6.6 Volt ) / 0.29e-3 A
t = 0.00005 sec
t = 50 µs
Dieses Ergebnis stimmt erstaunlich gut mit der Simulation überein:
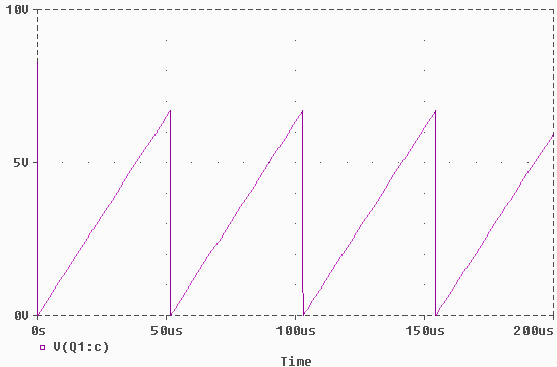
Simulation der Ausgangsspannung.
Laut der Simulation erhalten wir einen Wert von 51 µs für die Anstiegszeit.
Entladezeit des Kondensators: Durch den Timer NE 555 wird der Kondensator mit einem relativ hohen Strom von mindestens 35 mA entladen. Dadurch ergibt sich eine Entladezeit von maximal
t = (C·U) / I
t = ( 2.2e-9 F · 6.6 Volt ) / 35e-3 A
t = 0.0000004 sec
t = 0.415 µs.
Die Simulation hingegen kommt auf einen Wert in der Größenordnung von 0.3 µs, wie nachfolgendes Bild zeigt.
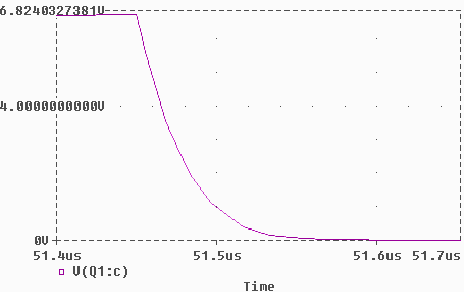
Entladekurve des Kondensators bei starker zeitlicher Dehnung betrachtet.
Auf jeden Fall liegt man auf der sicheren Seite, wenn man mit Entladeströmen in der Größenordnung von 35 – 50 mA rechnet. Damit man auch wirklich eine Sägezahnform erhält, sollte der Ladestrom wesentlich kleiner als der Entladestrom sein. Andernfalls erhält man ein Signal, das mehr einer Dreieckform ähnelt.
Triggerbarer Sägezahngenerator: Im Gegensatz zur vorangegangenen Schaltung wird ein Sägezahn-Impuls durch die abfallende Flanke eines Rechtecksignals am Pin 2 des NE555 ausgelöst.
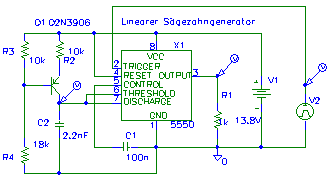
Pin 2 am NE555 ist hier als Triggerausgang ausgeführt. Getriggert wird mit der abfallenden Flanke.
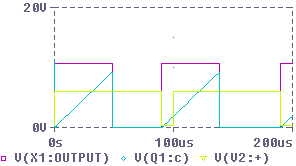
Grün: Triggersignal; Hellblau: Sägezahn am Kollektor des Transistors; Rosa: Rechteck am Pin 3 des NE555.
