Diese Schaltung unterscheidet sich nur an einer Stelle von der des Dreieckgenerators: Zusätzlich zu R10, welcher für den Ladestrom des Kondensators verantwortlich ist, befindet sich in Serie zu ihm noch die Diode D1 und parallel zu D1 der relativ hohe Widerstand R11.
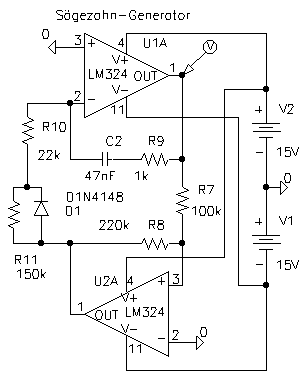
Sägezahngenerator.
Durch die Diode unterscheidet sich nun der Ladestrom vom Entladestrom. Die Folge ist, dass sich Anstiegs- und Abfallzeit unterscheiden. Das Ausgangssignal erhält ein sägezahnförmiges Aussehen.
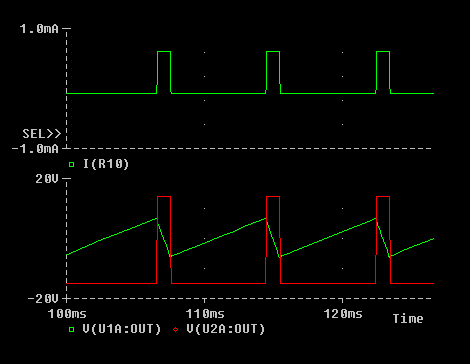
I durch R10 (oben) und Spannungen am Eingang und Ausgang des Schmitt-Triggers (unten).
In der obigen Abbildung sieht man in der oberen Hälfte den Strom I, welcher durch R10 fließt. Sein Betrag ist dann am höchsten, wenn auch die Umladezeit des Kondensators C2 am kürzesten ist. Unten sieht man als rote Rechtecklinie die Ausgangsspannung des Schmitt-Triggers und das Sägezahn-Signal am Ausgang des Integrators.
1. Fall. Das Ansteigen des Sägezahns
Ist die Spannung am Ausgang (Pin 1) des unteren Operationsverstärkers (U2A) negativ (siehe rotes, unteres Rechtecksignal), dann ist die Diode D1 gesperrt. Der Kondensator wird über R10 und R11 umgeladen (R9 darf man vernachlässigen). Es fließt ein geringer Strom I durch R10 und R11 in C2 hinein.
Die Anstiegszeit berechnet sich dann nach dem gleichen Verfahren wie bei dem Dreieckgenerator: Der Betrag des Ladestrom I1 ist dann
I1 = Ub / (R10 + R11)
I1 = 15 Volt / (22kOhm + 150 kOhm)
I1 = 15 Volt / 172 kOhm = 0.0872 mA
Nun können wir die Anstiegszeit t1 berechnen:
t1 = (C * U) / I1
t1 = (C * (UEIN – UAUS) / I1
t1 = (47e-9 F * (6.77 Volt – – 6.4 Volt)) / I1
t1 = (47e-9 F * (13.17 Volt)) / 0.0872 mA
t1 = 6.19e-7 F*V / 0.0872 mA
t1 = 7.098e-3 s = 7.1 ms
Die Anstiegszeit beträgt demnach 7.09 ms (Ergebnis der Simulation: 7 ms).
2. Fall. Das Abfallen des Sägezahns
Diesmal ist die Ausgangsspannung des Schmitt-Triggers im Gegensatz zum 1. Fall positiv. Das bedeutet, dass die Diode in Durchlassrichtung gepolt ist. Wir berücksichtigen bei der nachfolgenden Überlegung eine Dioden-Schwellenspannung von 0.6 bis 0.7 Volt. Dann fällt an R10 die Spannung Ub – 0.6 Volt ab (Genau genommen fließt noch ein sehr geringer Strom durch R11: IR11 = 0.6 Volt / 150 kOhm, den wir nicht berücksichtigen). Der Betrag von I2 ist dann
I2 = (Ub – 0.6 Volt) / R10
I2 = 14.4 Volt / 22kOhm
I2 = 0.65 mA
Dieser Strom ist wie zu erwarten wesentlich höher als I1. Nun können wir die Anstiegszeit t2 berechnen:
t2 = (C * U) / I2
t2 = (C * (UEIN – UAUS) / I2
t2 = (47e-9 F * (6.77 Volt – – 6.4 Volt)) / I2
t2 = (47e-9 F * (13.17 Volt)) / 0.65 mA
t2 = 6.19e-7 F*V / 0.65 mA
t2 = 9.52e-4 s = 0.952 ms
Das Abfallen des Sägezahns geschieht also in einer sehr kurzen Zeit von 0.952 ms (Ergebnis der Simulation: 0.97 ms).
