Die Kathodenbasisschaltung ist die wichtigste Schaltung mit Röhren, um die Grundlagen der Schaltungstechnik zu verstehen. Sie entspricht bei Feldeffekttransistoren der Source-Schaltung oder bei bipolaren Transistoren der Emitterschaltung.
Um zu verstehen, wie Röhrenschaltungen funktionieren, ist es erst einmal wichtig sich mit der Wirkungsweise von Elektronenröhren zu beschäftigen, welche ich unter „Wie funktionieren Elektronenröhren und ihre Schaltungstechnik“ erklärt habe.
Kathodenbasisschaltung mit einer Triode: Sie heißt Kathodenbasisschaltung, weil die Kathode der gemeinsame Anschluss für die Eingangs- und Ausgangswechselspannung ist.
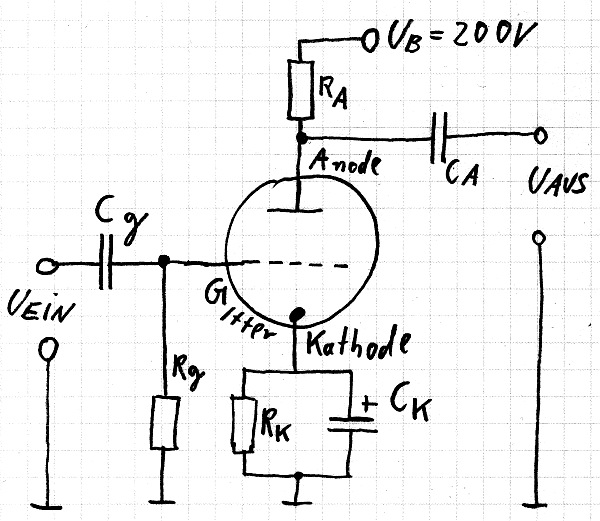
Kathodenbasisschaltung mit einer Triode: Cg = Koppelkondensator zum Steuergitter, Rk = Kathodenwiderstand, dessen Spannungsabfall für die negative Gittervorspannung sorgt, Rg = Gitterableitwiderstand, der dafür sorgt, dass die Elektronen, welche von der Kathode auf das Gitter fliegen, nach Masse abfließen können, CK = Kathodenkondensator. Er sorgt dafür, dass die Kathode wechselspannungsmäßig an Masse liegt. RA = Arbeitswiderstand, CA = Koppelkondensator für die gleichspannungsfreie Auskopplung des Ausgangssignals, UB = Betriebsspannung oder Anodenversorgungsspannung, UEin = Eingangswechselspannung, UAus = Ausgangswechselspannung.
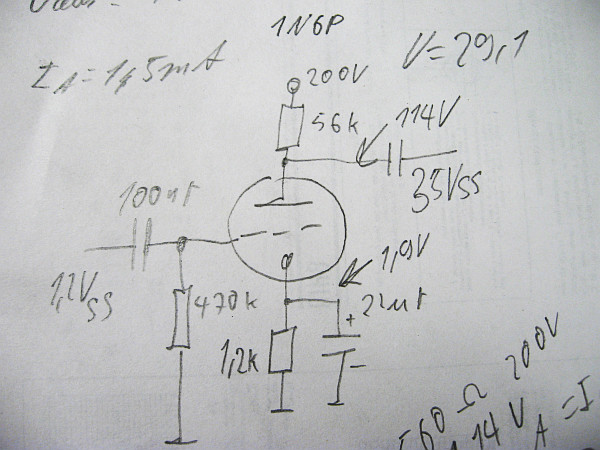
Kathodenbasisschaltung mit einer Triode (6N1P), Originalhandskizze.
Über den 100 nF-Kondensator wird die Eingangswechselspannung (1,2 Vss) dem Steuergitter der Triode zugeführt. Der Koppelkondensator (hier 100 nF) lässt nur die Wechselspannungsanteile durch. Der 470- kOhm-Widerstand zwischen Gitter und Masse verhindert, dass sich das Steuergitter durch anhaftende Elektronen, die von der Kathode kommen, negativ auflädt. Der fast nicht vorhandene Gitterstrom kann für weitere Betrachtachtungen vernachlässigt werden. Am 1,2-kOhm-Widerstand (Kathodenwiderstand) fallen 1,9 Volt ab, wodurch das Steuergitter gegenüber der Kathode um diesen Betrag negativ vorgespannt ist. Dadurch fließt praktisch kein Gitterstrom. Parallel zu diesem Kathodenwiderstand ist noch ein Kondensator geschaltet. Er sorgt dafür, dass wechselspannungsmäßig die Kathode mit der Masse verbunden ist.
Wechselspannungsverstärkung: Je weniger negativ das Steuergitter ist, desto mehr Elektronen fließen von der Kathode zur Anode. Es fließt also ein Anodenstrom in Abhängigkeit von der Gitterspannung. Für die Spannungsänderung am Steuergitter sorgt die Eingangswechselspannung. Der Anodenstrom ändert sich also im Takt der Eingangswechselspannung. Ist das Steuergitter weniger negativ, dann fließt mehr Anodenstrom und umgekehrt. Fließt mehr Anodenstrom, dann fällt am Arbeitswiderstand (56 kOhm), der zwischen der Anodenspannungsversorgung (200 Volt) und der Anode liegt, mehr Spannung ab. Folglich sinkt die Spannung an der Anode. Diese Spannung greifen wir als Ausgangsspannung ab. Daraus ergibt sich: Steigt die Gitterspannung an, dann sinkt die Anodenspannung und umgekehrt. Eingangs- und Ausgangsspannung sind also um 180° phasenverschoben. Damit die Ausgangsspannung frei von der überlagerten Anodengleichspannung ist, schalten wir einen Koppelkondensator dazwischen.
Anders erklärt: Steigt die Gitterspannung, dann steigt der Anodenstrom. Es fällt dann nach dem Ohmschen Gesetz mehr Spannung am Arbeitswiderstand ab. Dadurch sinkt die Spannung an der Anode.
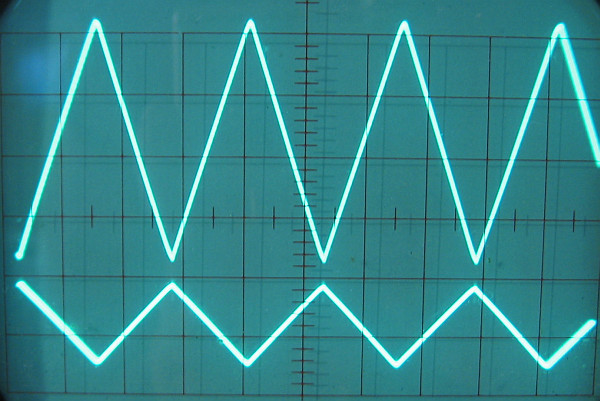
Unten ist die Eingangswechselspannung, oben die Ausgangswechselspannung. Immer, wenn die Gitterspannung steigt, fällt die Anodenspannung und umgekehrt. Um dies besser zu sehen, habe ich an den Eingang eine Dreieckspannung angelegt.
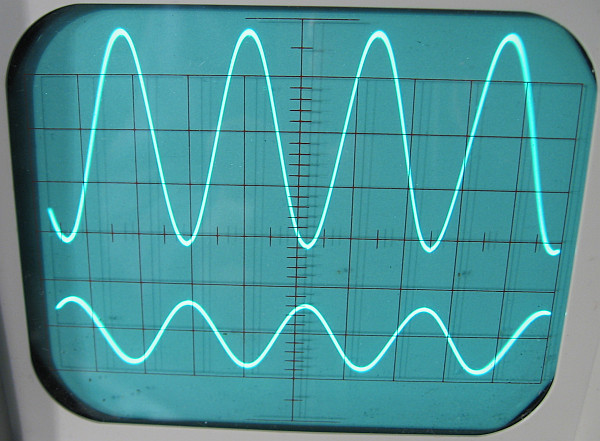
Hier derselbe Versuch mit einer Sinusspannung. Eingangsspannung 1,2 Vss, Ausgangsspannung 35 Vss (Vss ist die Spannung zwischen dem minimalen und maximalen Wert eines Kurvenzugs).
Arbeitspunkt: In Ruhe – also ohne Eingangsspannung – fließt bei dieser Schaltung ein Anodenruhestrom von 1,5 mA, was auch dem Strom durch die Kathode entspricht. An der Anode liegen in Ruhe etwa 114 Volt an, die ich gemessen habe. Das können wir leicht nachprüfen, denn bei einem Anodenstrom von 1,5 mA fallen an dem Arbeitswiderstand (56 kOhm) nach dem Ohmschen Gesetz 84 Volt ab. Die Anodenspannungsversorgung (200 Volt) minus dieser 84 Volt ergibt 116 Volt. Mein gemessener Wert stimmt als gut mit dem rechnerischen Wert überein. Der Arbeitspunkt der Röhre liegt also bei 1,5 mA Anodenstrom und 116 Volt Anodenspannung. Den Spannungsabfall am Kathodenwiderstand können wir vernachlässigen.

Versuchsaufbau: Vorderansicht. Anschlüsse von links nach rechts: Masse, Anodenspannung, Heizspannung.

Versuchsaufbau: Bestückungsseite.
Nachfolgend ein neues Rechenbeispiel mit der Berechnung aller Bauteile.
Ausgangskennlinienschar: Für die Dimensionierung der Schaltung ist die Ausgangskennlinienschar sehr hilfreich. Sie enthält praktisch alle Daten, die wir benötigen. Die Ausgangskennlinienschar finden wir im Datenblatt der Röhre 6N1P, die wir hier im Beispiel verwenden.
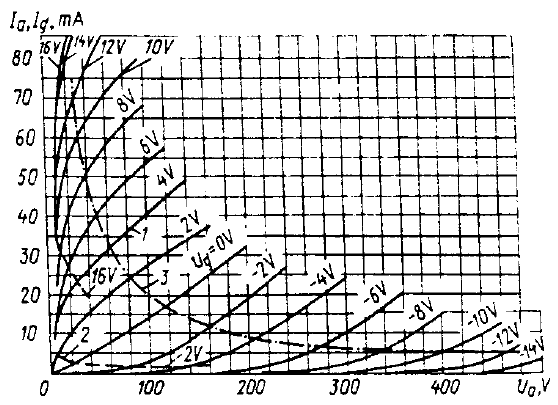
Ausgangskennlinienschar der NF-Triode 6N1P.
Auf der horizontalen Linie ist die Anodenspannung eingetragen und auf der vertikalen Linie der Anodenstrom. Für verschiedene Gitterspannungen ergeben sich verschiedene Ausgangskennlinien. Folgendes ist abzulesen: Je höher die Anodenspannung, desto höher ist auch der Anodenstrom. Je negativer bzw. niedriger die Gitterspannung, desto niedriger ist auch der Anodenstrom.
Arbeitsgerade: Angenommen wir verwenden als Arbeitswiderstand 10 kOhm und eine Anodenversorgungsspannung (Betriebsspannung) von 200 Volt.
1. Fall: Fließt durch die Anode kein Strom, weil die Gitterspannung sehr negativ ist, dann würde die volle Betriebsspannung von 200 Volt an der Anode anliegen, denn wenn kein Strom fließt, dann kann auch keine Spannung am Arbeitswiderstand abfallen.
2. Fall: Würden wir das Gitter theoretisch so positiv machen, dass überhaupt keine Spannung zwischen Anode und Kathode abfällt, dann könnten durch den Arbeitswiderstand und damit durch die Anode nach dem Ohmschen Gesetz I = U / R = 200 Volt / 10 kOhm = 20 mA Anodentrom fließen.
Wir haben damit zwei Punkte im Ausgangskennlinienfeld: 1. mit 20 mA Anodenstrom bei 0 Volt Anodenspannung und 2. 200 Volt Anodenspannung bei 0 mA Anodenstrom. Diese beiden Punkte können wir in das Ausgangskennlinienfeld eintragen und durch eine Gerade verbinden, womit wir die Arbeitsgerade erhalten haben:
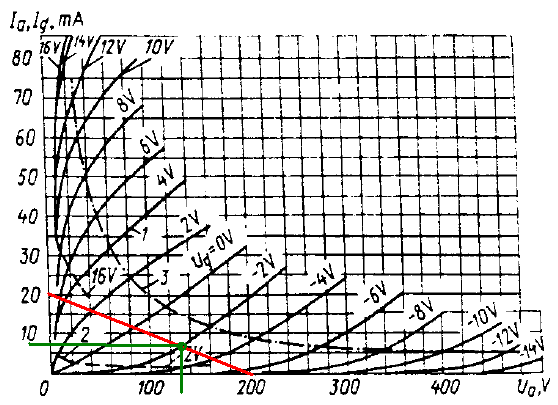
Die Arbeitsgerade des obigen Beispiels für einen Arbeitswiderstand Ra = 10 kOhm bei einer Betriebsspannung von 200 Volt ist rot eingezeichnet. Der grüne Punkt ist der Arbeitspunkt bei einer Gitterspannung von -2 Volt, fü den wir den Anodenstrom und die Anodenspannung ablesen können. Übrigens ist hier noch die Leistungshyperbel (3) im Ausgangskennlinienfeld eingetragen. Die Arbeitsgerade muss immer unterhalb dieser Hyperbel liegen, damit die maximal zulässige Anodenverlustleistung (Anodenstrom * Anodenspannung) niemals überschritten wird.
Im obigen Bild ist die Arbeitsgerade rot eingezeichnet. Sie schneidet also bei 200 Volt Anodenversorgungsspannung und einem Arbeitswiderstand von 10 kOhm die horizontale X-Achse bei 200 Volt und die vertikale Y-Achse bei 20 mA.
Arbeitspunkt und Anodenruhestrom: Wir können uns nun einen Arbeitspunkt auswählen, den ich für eine Gitterspannung von -2 Volt eingetragen habe. Demnach liegt der Anodenruhestrom bei etwa 7,5 mA, wobei etwa 130 Volt zwischen Kathode und Anode anliegen. Den zusätzlichen Spannungsabfall am Kathodenwiderstand habe ich bei dieser Betrachtung wieder vernachlässigt, da er nur 1% der Anodenversorgungspannung ausmacht. Diese 1% sind viel kleiner als die Exemplarstreungen der Röhrenparameter, welche bei 5 bis 10% liegen können.
Berechnung des Kathodenwiderstands: An ihm soll also die negative Gittervorspannung von 2 Volt abfallen, wenn ein Anodenruhestrom ( = Kathodenruhestrom) von 7,5 mA durch ihn fließt. Dann muss der Kathodenwiderstand R = U / I = 2 Volt / 7,5 mA = 266 Ohm haben. Wir wählen natürlich nicht 266 Ohm, sondern den nächst passenden, also 220 oder 270 Ohm.
Verlustleistungen der Widerstände berechnen: Die Verlustleistung P berechnet sich immer nach P = U * I, also dem Produkt aus der abfallenden Spannung mal dem durchfließenden Strom. Dabei reicht es die Mittelwerte zu verwenden. Wir brauchen also wegen der thermischen Trägheit der Widerstände nicht die Wechselspannungswerte zu berücksichtigen. Beim Kathodenwiderstand der verwendeten Schaltung ist die Verlustleistung 2 Volt *7,5 mA = 15 mW. Der Anodenwiderstand benötigt schon mehr Verlustleistung: 7,5 mA * 70 Volt = 525 mW. Die Verlustleistung des Gitterableitwiderstandes ist vernachlässigbar gering.
Ablesen der Spannungsverstärkung V: Würde die Gitterspannung zwischen 0 und -4 Volt schwanken, dann können wir eine Anodenspannungsänderung zwischen etwa 80 Volt und 160 Volt vom ablesen, wie es die hellblauen Linien im nachfolgenden Bild kennzeichnen. Die Spannungsversärkung wäre dann Ausgangsspannungänderung / Eingangsspannungänderung = ( 160 Volt – 80 Volt) / 4 Volt = 80 / 4 = 20. Das ist allerdings nur ein grober Wert, da wir die Röhre nicht mit 80 Vss aussteuern würden. Die Verstärkung einer Röhre ist für größere Signalpegel nicht mehr als linear zu betrachten. Nur um einen kleinen Bereich um den Arbeitspunkt herum kann eine Liniarität angenommen werden.
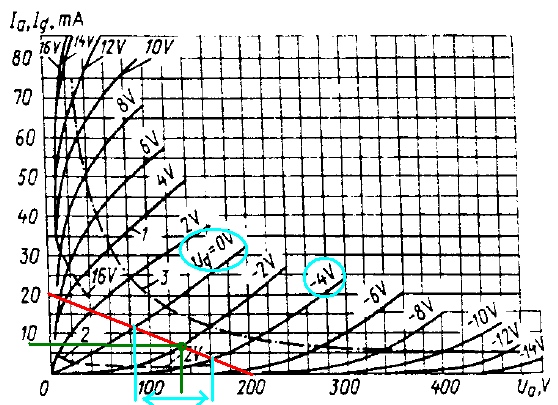
Ablesen der Anodenspannungsänderung, wenn sich die Gitterspannung zwischen 0 und -4 Volt ändern würde.
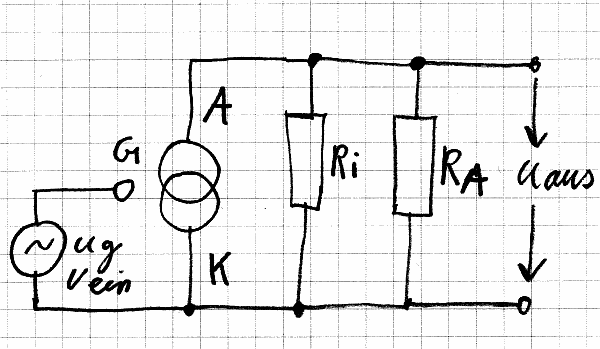
Ersatzschaltbild der Kathodenbasisschaltung, um die Wechselspannungsverhältnisse bei kleinen Auslenkungen um einen bestimmten Arbeitspunkt besser verstehen zu können.
Ersatzschaltbild einer Röhre: Siehe obiges Bild. Die Röhre wird als spannungsgesteuerte Stromquelle, symbolisiert durch die zwei Kreise, der noch der Innenwiderstand Ri parallel geschaltet ist, verstanden. Je höher die Wechselspannung zwischen Gitter und Kathode, desto mehr Wechselstrom fließt zwischen Anode und Kathode. Parallel zu dieser idealen Stromquelle liegt der Innenwiderstand Ri der Röhre und der Arbeitswiderstand Ra. Warum liegt Ra wechselspannungsmäßig wischen Anode und Kathode? Weil die Spannungsquelle für die Betriebsspannung (Anodenversorgungsspannung) im Idealfall einen sehr kleinen Innenwiderstand hat, der die Wechselspannung oder den Wechselstrom ungehindert durchlässt. Zwischen Plus und Minus der Betriebsspannung sitzt deshalb auch ein dicker, großer Elko, der für Wechselspannung einen geringen Widerstand darstellt.
Ausgangswiderstand Raus der Verstärkerschaltung: Den Ausgangswiderstand der Schaltung können wir auch leicht abschätzen. Er setzt sich zusammen aus der Parallelschaltung des Arbeitswiderstands Ra und des Innenwiderstands Ri der Triode. Leider ist Ri nicht im Datenblatt der 6N1P angegeben. Dafür ist die Steilheit S (Transconductance) mit 3,5 bis 5,5 mA/V angegeben. Der Mittelwert liegt also bei 4,5 mA/V. Außerdem ist der Amplificationfactor µ mit 35 plus minus 8 angegeben. Der Amplificationfactor ist der Kehrwert des Durchgriffs D. Nach der Barkhausenschen Röhrenformel ist
S * D * Ri = 1
Dann ist Ri = 1 / (S * D). Da µ der Kehrwert von D ist (also µ = 1/D), ist
Ri = µ / S.
Also ist Ri = 35 / 4,5 mA/V = 7,8 kOhm. Dies ist allerdings nur ein überschlägiger Wert, da Ri immer etwas vom Arbeitspunkt abhängig ist. Da wechselspannungsmäßig Ri (7,8 kOhm) parallel zum Arbeitswiderstand (10 kOhm) liegt, können wir mit einem Ausgangswiderstand Raus von etwa 4,4 kOhm rechnen. Dabei ist Raus die Parallelschaltung des Arbeitswiderstands Ra und dem Röhreninnenwiderstand Ri. Laut der Formel für die Parallelschaltung von Widerständen ist Raus = (Ra * Ri)/(Ra + Ri) = 4, 4 kOhm.
Berechnen der Spannungsverstärkung V: Das geht nach der Formel
V = S * Raus.
Dabei ist Raus wieder die Parallelschaltung des Arbeitswiderstands Ra und Ri. Laut der Formel für die Parallelschaltung von Widerständen ist Raus = (Ra * Ri)/(Ra + Ri) = 4, 4 kOhm.
Also ist V = 4,5 mA/V * 4,4 kOhm = 19,8. Das entspricht ja fast dem im Ausgangskennlinienfeld abgelesenen Wert.
Da in den meisten Datenblättern nur S und µ angegeben sind, aber nicht Ri, können wir durch Einsetzen und Umformen folgende Formel für die überschlägige Berechnung der Spannungsverstärkung V erhalten und verwenden:
V = (Ra * µ) / (Ra + (µ / S)).
Diese Formel ist jetzt schön unverständlich und nicht mehr bildhaft zu verstehen. Dafür ist sie aber bequem anzuwenden. Mathematik dient eben nicht zum Verständnis eines Zusammenhangs, wie viele glauben, sondern nur um eine möglichst exakte Beschreibung zu finden, um bei Vorgängen möglichst exakte Vorhersagen treffen zu können, ohne die Zusammenhänge im einzelnen unbedingt verstehen zu müssen. Deshalb ist die Mathematik so wichtig und unverzichtbar.
Maximaler Wert des Arbeitswiderstands Ra: Je höher wir den Arbeitswiderstand Ra wählen, desto höher wird die Verstärkung zum Preis eines höheren Ausgangswiderstands. Wollen wir eine maximale Spannungs-Verstärkung erhalten, reicht es nach einer Faustformel den Arbeitswiderstand Ra 8 mal so hoch wie den Innenwiderstand Ri zu wählen, denn eine weitere Erhöhung des Ra liefert keinen nennenswerten Vorteil, weil mit geringer werdenden Anodenstrom die Steilheit abnimmt. Ra wäre dann 8 * Ri = 62 kOhm.
Noch ein Rechentipp: Da S in mA / Volt angeben ist und Ra und Ri in kOhm, kommt immer die Spannung in Volt heraus, denn 1 Volt = 1 kOhm * 1 mA. Wir können also mit Ohm und Ampere rechnen oder mit kOhm und mA. Für die Strom- und Widerstandsverhältnisse in der Elektronik bietet sich das Rechnen mit mA und kOhm an.
Dimensionierung des Eingangskoppelkondensators: Der Koppelkondensator bildet zusammen mit dem Gitterableitwiderstand einen RC-Hochpass. Als NF-Verstärker soll die untere Grenzfrequenz fg bei 50 Hz liegen. Laut der Formel für RC-Tiefässe und RC-Hochpässe
fg = 1 / (2 * pi * R * C)
ist dann bei einem Gitterableitwiderstand von 470 kOhm der Koppelkondensator 6,8 nF groß. Wir nehmen dann 10 nF.
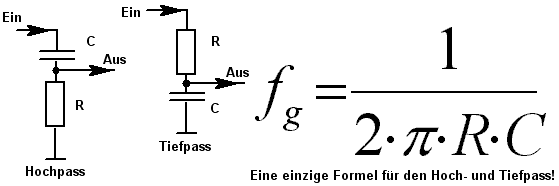
Formel für ein RC-Hoch- oder Tiefpass. Es sind die Grundeinheiten Hz, Farad und Ohm einzusetzen.
Dimensionierung des Kathodenkondensators: Das ist der Kondensator, der parallel zum Kathodenwiderstand liegt. Ohne diesen Kondensator hätten wir eine Stromgegenkopplung, welche die Spannungsverstärkung herabsetzt. Diese Gegenkopplung funktioniert so: Wenn die Gitterspannung positiver wird, dann fließt mehr Strom durch den Kathodenwiderstand. Also fällt auch mehr Spannung an ihm ab, was die Spannungsdifferenz zwischen Gitter und Kathode verringert und der Eingangsspannung entgegenwirkt. Diese Spannungsänderung am Kathodenwiderstand können wir durch einen genügend großen Kondensator parallel dazu glätten. Der Blindwiderstand des Kondensators sollte bei der niedrigsten zu übertragenden Frequenz (hier 50 Hz) etwa 1/5 des Kathodenwiderstands sein. Der Blindwiderstand Xc einer Kapazität ist
Xc = 1 / ( 2 * pi * f * C).
+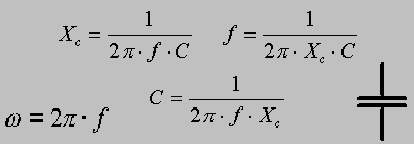
Formel für den Blindwiderstand Xc einer Kapazität. Es sind wieder die Grundeinheiten einzusetzen.
Bei einem Kathodenwiderstand von 270 Ohm kämen dann eine Kapazität von etwa 60 uF heraus. Wir wählen 100 uF.
Gemessene Werte: Die Schaltung habe ich nun mit folgenden Werten aufgebaut und gemessen: Ra = 10 kOhm, Rk = 270 Ohm; UA = 143 Volt, UB = 200 Volt, Ig = -1,6 Volt, IA = 5,8 mA; Uein = 1 Vss; Uaus = 20 Vss, V = 20. Die Abweichungen lassen sich unter anderem durch die Exemplarstreuungen der Röhren erklären. Die Spannungsverstärkung V entspricht genau dem erwarteten Wert.
Dynamische und statische Steilheit: Der hier vorgestellte Rechenweg kommt ausnahmslos mit der statischen Steilheit S aus. In der Röhrenliteratur kommt aber oft zur Verwirrung der Begriff der dynamischen Steilheit Sd vor, weshalb ich ihn hier vorstelle, obwohl er nicht unbedingt notwendig wäre. Es handelt sich hier nur um eine andere Darstellungsweise, wenn ein Arbeitswiderstand Ra ins Spiel kommt.
Die satische Steilheit S ist die Steilheit, die wir messen, wenn wir die Anodenspannung konstant halten. Angenommen wir haben eine Anodenspannung von 100 Volt. Nun ändern wir die Gitterspannung um 1 Volt und stellen zum Beispiel eine Anodenstromänderung von 5 mA fest, dann haben wir eine statische Steilheit von 5mA/Volt gemessen. Wohl gemerkt haben wir die Spannung zwischen Kathode und Anode konstant auf 100 Volt gehalten.
Bei der dynamischen Steilheit berücksichtigen wir die Verwendung eines Arbeitswiderstands Ra, der dafür sorgt, dass mit zunehmenden Anodenstrom die Anodenspannung sinkt. Die dynamische Steilheit Sd ist immer kleiner als die statische Steilheit S. Der Zusammenhang zwischen Sd und S ist wie folgt.
Sd = S * ( Ri / (Ri + Ra)).
Die dynamische Steilheit gilt immer für einen bestimmten Arbeitswiderstand Ra. Manchmal sind in den Röhrendatenblättern die dynamischen Steilheits-Kennlinien für verschiedenene Arbeitswiderstände angegeben. Die Spannungsverstärkung V können wir nämlich sehr bequem auch mit Hilfe der dynamischen Steilheit Sd berechnen:
V = Sd * Ra.
Auf die obige Formel kommen wir, wenn wir Sd = S * ( Ri / (Ri + Ra)) auf der rechten und linken Seite mit Ra erweitern bzw multiplizieren. Ein niedriges Ri sorgt für eine geringere dynamische Steilheit. Für eine hohe Spannungsverstärkung wollen wir also Röhren mit einem hohen Ri und einem hohen S haben.
Bei einer Pentode dürfen wir den Innenwiderstand Ri als fast unendlich hoch annehmen. Dann wird der Ausdruck Ri / (Ri + Ra) fast zu 1 und die dynamische Steilheit kann zur Vereinfachung mit der statischen Steilheit S gleichgesetzt werden.
Übrigens lassen sich die dynamische Steilheit Sd und die statische Steilheit S auf grafischen Wege mit Hilfe des Ausgangskennlinienfeldes ermitteln. Hier ist das Ausgangskennlinienfeld einer Triode vorgestellt.
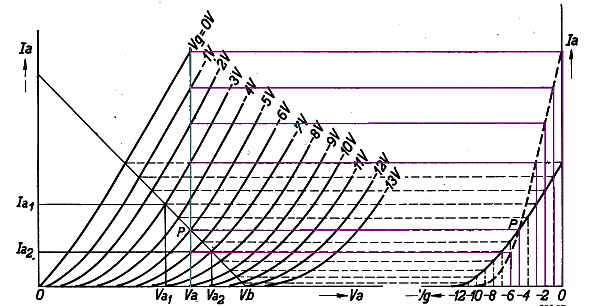
Ermittlung der statischen Eingangskennlinie (rechts, gestrichelt) aus dem Ausgangskennlinienfeld (links, x-Achse=Gitterspannung, y-Achse=Anodenstrom). Bei der Anodenspannung Va (grüne, senkrechte Linie) im Ausgangskennlinienfeld werden an den Schnittpunkten mit den Ausgangangskennlinien die jeweiligen Anodenströme für die verschiedenen Gitterspannungen abgelesen, um die Eingangskennlinie für eine Anodenspannung Va zu erhalten. Dazu dienen die violetten Hilfslinien.
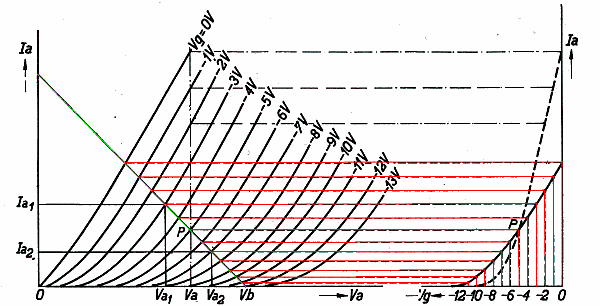
Ermittlung der dynamischen Eingangskennlinie. Hier wurde mit Hilfe der roten Hilfslinien die dynamische Eingangskennline (durgezogene Kurve, rechts) ermittelt. Im Prinzip funktionert das wie bei der Ermittllung der statischen Eingangskennlinie, allerdings werden jetzt die Anodenströme nicht mehr bei der konstanten Spannung Va abgelesen, sondern an der grün hervorgehobenen Arbeitsgeraden.
Die beiden Grafiken wurden einer Triode entnommen. Wir sehen, dass die statische Eingangskennlinie (gestrichelt) viel steiler verläuft als die dynamische Eingangskennlinie (durchgezogene Kurve). Hätten wir eine Pentode, würden wegen des hohen Innenwiderstands Ri die Ausgangskennlinien fast waagrecht verlaufen, woran man erkennen könnte, dass bei einem unendlich hohen Ri kein Unterschied zwischen der statischen und dynamische Steilheit existiert.
Austausch der 6N1P gegen die wesentlich steilere PCC88: Nun habe ich die 6N1P durch eine PCC88 ersetzt, denn die PCC88 hat eine Steilheit von 12,5 mA/V und die 6N1P hat nur 4,5 mA/V. Wie erwartet stieg der Anodenstrom etwas an, und zwar von 6 auf 8 mA. Ob die Röhre mit der Sollspannung von 7,6 Volt oder mit 6,3 Volt Heizspannung betrieben wird, hatte einen kaum messbaren Einfluss auf den Anodenstrom oder auf die Verstärkung.
Im ersten Moment hatte ich mich über die Spannungs-Verstärkung sehr gewundert, denn die lag bei der PCC88 nur bei 22. Sie ist also um nur 10% besser, obwohl die PCC88 fast 3-mal so steil ist. Ein Blick ins Datenblatt erklärt die Sache. Die PCC 88 hat ein µ = 33. Daraus lässt sich der Ri = µ / S errechnen, der bei 2,64 kOhm liegt, während die 6N1P ein Ri von 7,8 kOhm hat. Mit der bekannten Formel für die Spannungsverstärkung
V= S * ((Ra + Ri)/(Ra * Ri))
ergibt sich dann ein V=25. Also wundert mich demnach die gemessene Spannungverstärkung von 22 nicht mehr, die im Rahmen der Toleranz liegt.
Die PCC88 oder ECC88 ist wegen ihres relativ geringen Innenwiderstands für Audioanwendungen nicht besonders vorteilhaft gegenüber der 6N1P. Es bringt nichts in einem NF-Verstärker eine 6N1P gegen eine ECC88 auszutauschen. Die 0,8 dB mehr an Spannungsverstärkung wird mit Sicherheit fast niemand im Vergleich hören können. Selbst 3 dB hört man fast nicht. Es mögen sich vielleicht die frequenzabhägingen Gegenkopplungsverhältnisse ändern, wodurch der Verstärker etwas anders klingt, was dann aber Geschmackssache ist.
Einfluss der Betriebsspannung auf die Spannungsverstärkung: Ich habe bei der 6N1P die Versorgungsspannung von 200 auf 100 Volt heruntergedreht und die Spannungsverstärkung ist auch fast gleich geblieben. Das war auch zu erwarten, denn in der Formel V= S * ((Ra + Ri)/(Ra * Ri)) kommen die Versorgungsspannungen oder abgeleitete Werte nicht vor. Natürlich ändert sich S im Abhängigkeit vom Arbeitspunkt und damit indirekt von der Versorgungsspannung, aber der Einfluss fällt kaum ins Gewicht. Erst ab unter 80 Volt ging die Spannungsverstärkung herunter und dann wurde das Ausgangsignal durch die Begrenzung verzerrt. Das erklärt auch warum Allstromgeräte auch bei 110 Volt Anodenspannung noch gut funktionieren, allerdings ist die NF-Ausgangsleistung dann schwächer. Und wer eine Gleichrichterröhre austauscht nur weil die Betriebsspannung um 20 Volt gesunken ist, wird die neue Gleichrichterröhre wenn überhaupt nur dann merken, wenn er die Lautstärke ordentlich aufdreht.
Varianten der negativen Gittervorspannungserzeugung: Die Gittervorspannung kann auch ohne den Kathodenwiderstand erzeugt werden, indem der Gitterableitwiderstand so hoch gewählt wird ( meistens 22 – 56 MegOhm), dass sich eine negative Gittervorspannung einstellt. Dies wird sehr oft in Röhrenradios beim Triodensystem der EABC80 ausgeführt, die als NF-Eingangsröhre dient. Eine andere Variante ohne Kathodenwiderstand ist auch üblich, wenn die negative Regelspannung für die negative Gittervorspannung sorgt. Dies sieht man z.B. beim Heptodensysem der ECH81 oder bei der ZF-Regelpentode EF89. Je negativer die Gittervorspannung, desto geringer die Verstärkung.
Schließlich sieht man oft Radioschaltungen, bei denen der Minus-Anschluss des Netzteils über einen 100-Ohm-Widerstand mit der Masse verbunden ist. Diesem Widerstand ist noch ein 100 uF-Kondensator parallel geschaltet. Der Spannungsabfall dieses Widerstands dient dann für die negative Gittervorspannung mehrerer Röhren (z.B. beim Saba Wildbad W5). Der gesamte Strom für die Anoden aller Röhren von etwa 65 mA fließt dann über diesen Widerstand und erzeugt einen Spannungsabfall von 6,5 Volt. Sind die Elkos des Netzteils ausgetrocknet und haben nicht mehr genügend Kapazität, dann sind die Versorgungsspannungen nicht mehr stabil. Insbesondere ist dann die negative Vorspannung, die allen Röhren zugeführt wird, im Takt der NF schwankend. Man kann sich denken, dass dies zu den merkwürdigstens Effekten wie Pumpen oder Motorboating führen kann.
Pentode, Tetrode und Triode: Die hier genannten Überlegungen sind auch für eine Pentode gültig, wobei sich der Rechenweg noch vereinfacht, da bei einer Pentode der Innenwiderstand so hoch ist, so dass er vernachlässigt werden kann.
Für eine Tetrode können wir diesen Rechenweg auch nutzen. Bei der Wahl des Arbeitspunktes müssen wir aber aufpassen, dass der Mindestwert der momentanen Anodenspannung (meist bei 70 bis 90 Volt in Abhängigkeit von der gewählten Schirmgitterspannung) zu keinem Zeitpunkt unterschritten wird, da sonst die Tetrode in den instabilen Bereich gerät, was zu Verzerrungen führt. Die Tetrode kann deshalb nicht so hoch ausgesteuert werden und benötigt dadurch höhere Anodenspannungen als die Pentode.
Varianten des Arbeitswiderstands: Dieser muss kein reiner Ohmscher Widerstand sein, wie er hier im Beispiel des NF-Vorverstärkers verwendet wird. In einem ZF- oder HF-Verstärker kann er durch einen Parallelschwingkreis ersetzt werden. Dann hat er in Resonanz seinen höchsten Widerstand, der hauptsäclich durch die Kreisgüte bestimmt wird, wodurch die höchste Verstärkung auf der Resonanzfrequenz erzielt wird. Damit haben wir einen frequenzselektiven Verstärker, für die gerne Pentoden eingesetzt werden, weil 1. bei Pentoden durch die Abschirmung des Schirmgitters Eingang und Ausgang entkoppelt sind, was eine Neutralisation erübrigt und 2. weil der Innenwiderstand der Pentode besonders hoch ist, weshalb der Schwingkreis durch diesen Innenwiderstand kaum bedämpft wird. Das höhere Eigenrauschen der Pentode fällt kaum ins Gewicht, wenn durch die Vorstufen der Signalpegel bereits genügend angehoben worden ist.
Der Arbeitswiderstand kann auch ein Übertrager sein, wenn Leistungsanpassung notwendig wird, wie dies zum Beispiel bei der NF-Endstufe der Fall ist, bei der der niederohmige Lautsprecher ( 8 Ohm ) an den viel höheren Innenwiderstand der Pentode angepasst werden muss.
Gegenkopplungen: Über RC-Glieder (Kombinationen aus Widerständen und Kondensatoren) könnten wir einen Teil der Ausgangsspannung frequenzabhängig dem Eingang zurückführen, was sogar über mehrere Stufen geschehen kann. Wenn dies gegenphasig geschieht, werden bestimmte Frequenzen weniger stark verstärkt, was für die Klangeinstellung genutzt wird. Außerdem nehmen die Verzerrungen durch eine Gegenkopplung ab. Solche RC- und Gegenkopplungsglieder können einen einfachen NF-Verstärker auf den ersten Blick unübersichtlich erscheinen lassen.
Oszillator: Die Grundschaltung der Kathodenbasisschaltung kann auch als Oszillator dienen, wenn ein Teil der Ausgangsspannung dem Eingang wieder zurückgeführt wird. Wenn die Phasenlage und Amplitude entsprechend ist, fängt der Verstärker an zu schwingen und wir erhalten ein Oszillator, der ein gesondertes Kapitel verdienen würde.
Fazit: Mit dem Ohmschen Gesetz und ein paar einfachen Standardformeln des elektrotechnischen Grundwissens lässt sich mit Hilfe des Röhrendatenblatts eine Kathodenbasisschaltung recht einfach überschlägig berechnen. Mit zunehmend höheren Frequenzen müssen bei der Verstärkungsbetrachtung allerdings die Elektrodenkapazitäten mehr und mehr berücksichtigt werden. Ab etwa 100 MHz spielt sogar die endliche Geschwindigkeit der im Vakuum der Röhre fliegenden Elektronen eine deutliche Rolle.
